Kantitatif tahmin yöntemleri, geçmiş verileri kullanarak gelecekteki verilerin talep tahminlerini istatiksel olarak hesaplayabilmemizi sağlar. Talebin oluşmasına etki eden faktörler ile talep miktarı arasındaki ilişkinin gelecekteki dönemler için de aynı şekilde eğilim göstereceği varsayımına dayanmaktadır.
Bu modeller, eldeki en son gözlem değerinin bir sonraki dönem için en iyi öngörü değeri olarak alınabileceği varsayımını yapan modellerdir. Naive modellerinin en basiti ∧ Y t+1 = Yt………….(1) formülü ile öngörü değeri belirleyen modeldir. Bu modele göre hesaplanacak öngörü değerleri Yt’deki değişimleri çok yakından izler.
Zaman Serileri Analizi- Ortalama Yöntemleri
Basit ortalama yöntemi geçmiş dönem verilerinin tek tek toplanıp dönem sayısına bölünmesidir (Çağlar, 2007: 34). Yöntemin avantajı bütün dönemleri kullanarak tahminde düzleşme sağlaması ve kolay uygulanabilmesidir.
Ağırlıklı hareketli ortalama yönteminde dönemlere farklı (eşit olmayan) ağırlıklar uygulanabilir. Örneğin, son dönemdeki verilerin yapılacak tahminde daha etkili olacağı düşünülüyorsa, bu dönemlere daha fazla ağırlık verilebilir.
Ağırlıklı hareketli ortalamanın hesaplanması, seçilen dönemlerin talep miktarı, verilen ağırlıkla çarpılır, bu çarpımlar toplanır ve ağırlıkların toplamına bölünerek elde edilir (Taşdemir, 2012: 27). Bu yöntem hesaplanırken dönemlere verilen ağırlık 0-1 arasında değişmektedir verilen ağırlıkların toplamı 1 olur (İlhan, 56: 2015).
Üssel Düzeltme Yöntemi
Tek üssel düzeltme yöntemi tahmin etme gereksinimi çok sık olduğunda ve tahminin çokhızlı yapılması gerektiğinde etkin olan bir ağırlıklandırılmış hareketli ortalama tekniğidir. Tek üssel düzletmeyi uygulayabilmek için sadece üç veriye ihtiyaç vardır ve bu yöntemi güncellemek kolaydır. Gerekli veriler; geçmiş gözlem, son gözlem ve düzeltme katsayısı veya sabitidir (Taşdemir, 2012: 28).
Nedensel Yöntemler
Nedensel tahminleme yöntemi bağımlı değişkenin (tahmin edilmek istenen ürünün zaman içindeki satışları) birden çok değişkenin etkilediği düşünülen durumlarda kullanılabilir.
Regresyon ve korelasyon analizinde açıklanan istatiksel yöntemler kullanılarak bu değişkenlerin etkileri tahmine yansıtılmaya çalışılır (Özsoy, 2006: 43).
Regresyon Yöntemi
Regresyon analizi, bilinen bulgulardan, bilinmeyen gelecekteki olaylarla ilgili tahmin yapılmasında kullanılır. Regresyon, bağımlı ve bağımsız değişken(ler) arasındaki ilişkiyi ve doğrusal eğri kavramını kullanarak, bir tahmin eşitliği geliştirir (Köse, 2008: 3). Regresyon denklemi yardımıyla bağımlı değişken ile bağımsız değişkenler arasındaki ilişkiyi kuran parametrelerin değerleri tahmin edilir.
Temel amaç; X bağımsız değişkeni ile Y bağımlı değişkeni arasındaki doğrusal ilişkiyi Y = a + bX denklemi ile ifade etmek üzere bu denklemin parametrelerini (a ile b’nin alacağı değerler) bulmaktır.
Bağımlı değişkenin (Y) birden fazla bağımsız değişken (X1, X2, X3,…) tarafından etkilendiği bu gibi durumlarda, bağımsız değişkenler ile bağımlı değişken arasındaki doğrusal ilişkiyi (var ise) bulmak için çoklu doğrusal regresyon yöntemi kullanılır. Bu yöntem, mantık olarak, basit doğrusal regresyon yöntemine benzemekle birlikte, bulunması gereken parametrelerin fazlalığı nedeniyle oldukça karmaşıktır.
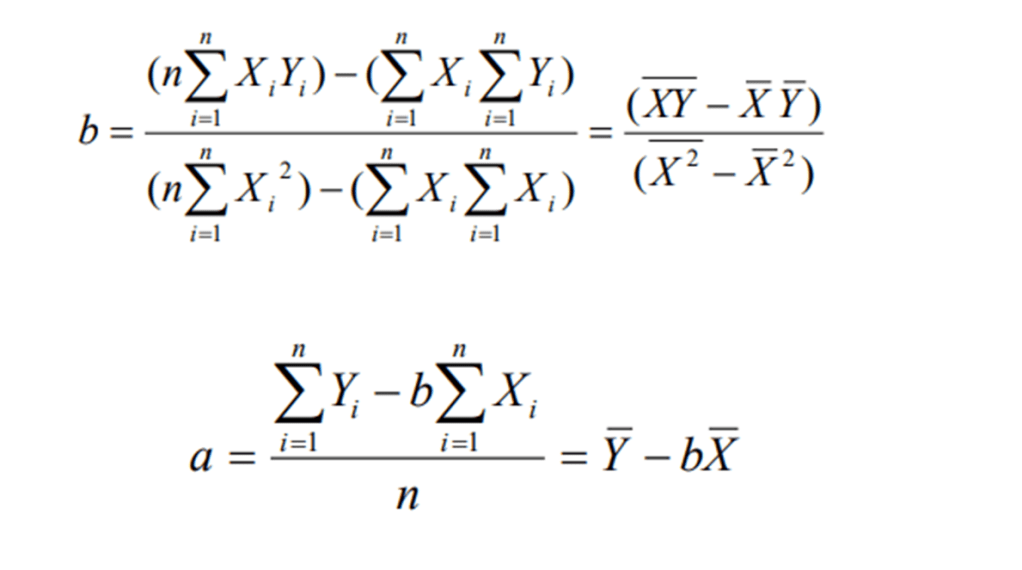
Deneysel verilerin doğrusal bir eğriye ne kadar iyi uyduğunun en iyi ölçütü, regresyon analiz işleminde hesaplanmış “determinasyon katsayısıdır (R2 ).” n R2 = 1 olması, deneysel verilerin kusursuz bir doğrusal eğri sağlandığının kanıtıdır. Ne kadar çok veri noktası varsa, R2 ’nin güvenirliği o kadar yüksektir.
Ekonomi ve işletmecilik alanlarında herhangi bir bağımlı değişkeni tek bir bağımsız değişken ile açıklamak mümkün değildir. Ekonomik modeller, genellikle birden fazla sebebin sonucudurlar. Çok fazla sayıda değişken bir araya gelerek bir diğer değişkeni etkileyebilmektedirler. Bu değişkenler aynı zamanda kendi aralarında da birbirlerini etkileyebilmektedir.
Bu sebeple, bu tür birden fazla değişkenin kullanılması gereken durumlarda tekli regresyon analizi yapılması mümkün değildir. Birden fazla bağımsız değişken kullanılarak yapılan regresyon analizine “çoklu regresyon analizi (multiple regression analysis)” adı verilmektedir.
İnterpolasyon genelde mühendislik ve deneylere/ölçümlere dayalı benzeri bilim dallarında, toplanan verilerin bir fonksiyon eğrisine uydurulması amacıyla kullanılmaktadır. Elde toplanan verinin dağınık ve özellikle aşırı heterojen olduğu durumlarda interpolasyon ile boş alanlardaki değerlerin bulunması önem kazanmaktadır.
Doğrusal ektrapolasyon bilinen verilerin sonunda bir teget doğrusu yaratıp bu doğruyu bu sınırdan daha ileriye uzatmak suretiyle elde edilir. Doğrusal ektrapolasyonun iyi sonuçlar vermesi şartları bilinen verilerin yaklaşık olarak doğrusal değişmeleri ve ektrapolasyonun bilinen verilerden cok daha uzak olmamasıdır.
Korelasyon
Korelasyon, olasılık kuramı ve istatistikte iki rassal değişken arasındaki doğrusal ilişkinin yönünü ve gücünü belirtir. Genel istatistiksel kullanımda korelasyon, bağımsızlık durumundan ne kadar uzaklaşıldığını gösterir.
Farklı durumlar için farklı korelasyon katsayıları geliştirilmiştir. Bunlardan en iyi bilineni Pearson çarpım-moment korelasyon katsayısıdır.
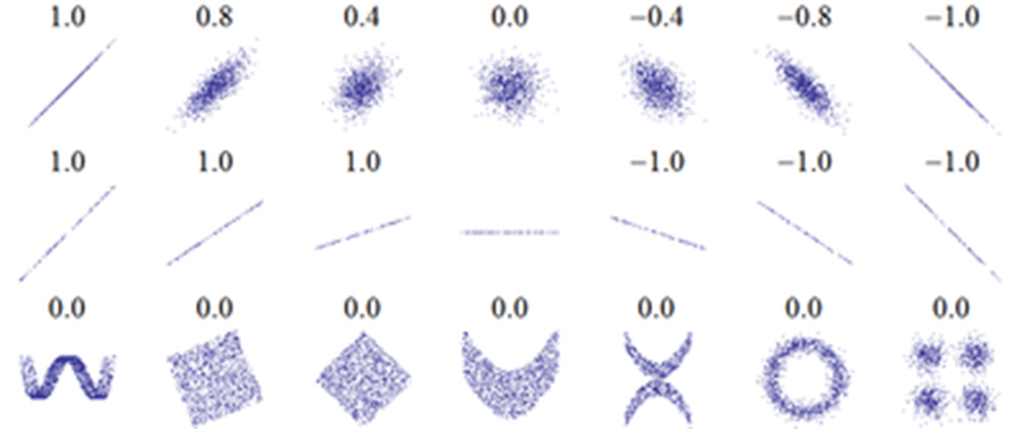
İstatistikte korelasyon hakkında çok kullanılan ve her istatistik kullananın bilmesi gerek bir cümle şudur:
Korelasyon veya doğrusal ilişki nedensellik değildir.
Genellikle çok kişi iki değişken arasında bir ilişki kurulunca birinin sebep diğerinin sonuç olduğuna ve birinin diğerine neden olduğuna inanmış görünürler. Gerçekten nedensellik ve korelasyon birbirine bağlı kavramlardır:
Nedensellik ispat edilmesi için korelasyonun bulunması gereklidir ama bu nedensellik göstermek için yeterli değildir. Nedensellik ve korelasyon birbirlerine eşit değillerdir ama daha uygun cümleler ile;
Ampirik olarak gözlemlenen birlikte değişme nedensellik açıklaması için gereklidir ama yeterli değildir.
Korelasyon nedensellik değildir; ama nedenselliğin daha ayrıntılı incelenmesini gerektiren ipucunu sağlar. İskandinavya’da 19. yüzyıl sonu ve 20. yüzyıl için yıllık leylek sayısı ve yıllık çocuk doğumları inceleyince çok yakın bir pozitif korelasyon bulunmaktadır. Bu, doğan çocukların leylekler tarafından getirildikleri önermesini doğrulamaz. Hem çocuk doğum sayısı hem de leylek sayısı ekonomik gelişme ve şehirleşme dolayısıyla azalmış ve bu iki azalma birinin diğerine sebep-sonuç olmasından ortaya çıkmamıştır.
Bir sahil şehrinde aylık dondurma satışları ile aylık denizde boğulma sayıları yıl içinde birlikte artıp eksilme gösterip yakın pozitif korelasyon gösterirler. Bu demek değildir ki fazla dondurma fazla boğulmalara sebep-sonuç olmakta veya boğulmaların azalması dondurma satışlarına aksi tesirde bulunmaktadır. Her ikisi de mevsim değiştiği için aynı yönde değişik etki görmektedir.
Ayakkabı ile uyumak, baş ağrısı ile uyanmakla yakın pozitif korelasyon gösterir. Bu demek değildir ki ayakkabı ile yatmak baş ağrısı doğurur. Çok daha uygun bir açıklama, her ikisinin de fazla alkollü içki kullanımı sonucu ortaya çıkmasıdır.
Kaynakça
Akgül, Barış (2010). Türkiye’deki Otomotiv Sektörü ve Örnek Bir Talep Tahmin Çalışması. İşletme Yönetimi Bilim Dalı, Yıldız Teknik Üniversitesi Fen Bilimleri Enstitüsü, İstanbul
Çağlar, Tarık (2007). Talep Tahmininde Kullanılan Yöntemler ve Fens Teli Üretimi Yapan Bir İşletme Uygulaması, Yüksek Lisans Tezi, Kırıkkale Üniversitesi Fen Bilimleri Enstitüsü, Kırıkkale.
Demirbaş, Fidan Pınar (2011). Kombi Üretiminde Talep Tahmin Yöntemlerinin Uygulanması. Yüksek Lisans Tezi, Kocaeli Üniversitesi Fen Bilimleri Enstitüsü, Kocaeli.
Sevgen, S. (2015). Sağlık Hizmetleri Talep Tahmini: Adana İli Hastane Uygulaması. Yüksek Lisans Tezi, İşletme Yönetimi Programı, Atılım Üniversitesi Sosyal Bilimler Enstitüsü , Ankara.
Ünüvar, Ali (1995). Üretim Yönetimi ve Organizasyonu (Fabrika Organizasyonu) Ders Notları. Konya.
Üreten, Sevinç (1999). Üretim İşlemler Yönetimi (2. Baskı). Ankara: Nobel Yayınları.
Kılınç, Günay (2015). Yapay Sinir Ağları ile Yemekhane Günlük Talep Tahmini. Yüksek Lisans Tezi, Bilgisayar Mühendisliği Bölümü, Pamukkale Üniversitesi Fen Bilimleri Enstitüsü, Denizli.
Kobu, Bülent (1999). Üretim Yönetimi (10. Baskı). İstanbul: Beta Baskı.
Meydan, Yusuf Ali (2007). Talep Tahmin Yöntemleri ve Orta Ölçekli Bir İşletmede Uygulaması, Yüksek Lisans Tezi, İstanbul Ticaret Üniversitesi Fen Bilimleri Enstitüsü, İstanbul.
Özsoy, Ersöz (2006). Talep Tahminine Dayalı Müşteri Odaklı Üretim Planın Oluşturulması ve Bir Uygulama. Yüksek Lisans Tezi, Üretim Yönetimi ve Endüstri İşletmeciliği Programı, Dokuz Eylül Üniversitesi Sosyal Bilimler Enstitüsü, İzmir.
Olgun, Senem (2009). Tedarik Zinciri Yönteminde Talep Tahmini Yöntemleri ve Yapay Zeka Tabanlı Bir Talep Tahmini Modelinin Uygulanması, Yüksek Lisans Tezi, İstanbul Üniversitesi Fen Bilimleri Enstitüsü, İstanbul.
Yamak, Oygur (2007). Üretim Yönetimi (1. Baskı), İstanbul: Nobel Yayıncılık.
Yavuz, Alpagut. Talep Tahminleri Sunumu
http://www.mku.edu.tr/files/339-fe1f52d7-578f-4b4f-b078-bbcbae358b91.pdf
Erdem, İsmail. Ders Sunusu
