Paranın zaman değeri, bir miktar parayı daha sonra almaktansa şimdi almanın daha büyük fayda sağlayacağı yönündeki yaygın kabul gören varsayımdır. Paranın zaman değeri, para biriktirmek ya da yatırım yapmak yerine harcama yapmanın fırsat maliyetlerini tartarken dikkate alınan faktörler arasındadır. Bu nedenle, faizin ödenmesinin veya kazanılmasının nedenleri arasındadır: faiz, ister banka mevduatı ister borç olsun, mevduat sahibinin veya borç verenin paralarını kullanma kaybını telafi eder.

Yatırımcılar paralarını şimdi harcamaktan ancak gelecekte yatırımlarından olumlu bir net getiri bekledikleri takdirde vazgeçmeye isteklidirler, öyle ki daha sonra elde edilecek değer artışı hem şimdi para harcama tercihini hem de (varsa) enflasyonu dengeleyecek kadar yüksektir.
Paranın bir zaman değeri vardır çünkü zaman içinde daha fazla para kazanabilir (kazanma gücü). Paranın bir zaman değeri vardır çünkü satın alma gücü zaman içinde değişir (enflasyon). Paranın zaman değeri faiz oranı ile ölçülür. Faiz paranın maliyetidir – borç alan için bir maliyet ve borç veren için bir kazançtır.
Paranın zaman değeri problemleri, zamanın farklı noktalarındaki nakit akışlarının net değerini içerir.
Tipik bir durumda, değişkenler şunlar olabilir: bir bakiye (bir borcun veya bir finansal varlığın parasal birimler cinsinden reel veya nominal değeri), dönemsel bir faiz oranı, dönem sayısı ve bir dizi nakit akışı. (Bir borç söz konusu olduğunda, nakit akışları anapara ve faiz ödemeleridir; bir finansal varlık söz konusu olduğunda, bunlar bakiyeye yapılan katkılar veya bakiyeden çekilen tutarlardır). Daha genel olarak, nakit akışları periyodik olmayabilir ancak ayrı ayrı belirtilebilir.
Bu değişkenlerden herhangi biri belirli bir problemde bağımsız değişken (aranan cevap) olabilir. Örneğin, faizin dönem başına (aylık, diyelim) %0,5 olduğu; dönem sayısının 60 (ay) olduğu; başlangıç bakiyesinin (bu durumda borcun) 25.000 birim olduğu ve nihai bakiyenin 0 birim olduğu bilinebilir. Bilinmeyen değişken, borçlunun ödemesi gereken aylık ödeme olabilir.
Örneğin, bir yıl boyunca yatırılan ve %5 faiz kazanan 100 USD bir yıl sonra 105 USD değerinde olacaktır; dolayısıyla, enflasyonun yüzde sıfır olacağını varsayarak %5 faiz bekleyen bir alıcı için şimdi ödenen 100 USD ile tam bir yıl sonra ödenen 105 USD’nin her ikisi de aynı değere sahiptir. Yani, bir yıl boyunca %5 faizle yatırılan 100 USD, enflasyonun yüzde sıfır olacağı varsayımı altında gelecekteki değeri 105 USD’dir.
Bu ilke, gelecekteki olası bir gelir akışının, yıllık gelirlerin iskonto edilip daha sonra birbirine ekleneceği ve böylece tüm gelir akışının toplu bir “bugünkü değerini” sağlayacak şekilde değerlenmesine olanak tanır; paranın zaman değerine ilişkin tüm standart hesaplamalar, paranın zaman değerine eşit bir miktarla bugüne “indirgenmiş” gelecekteki bir toplamın bugünkü değerine ilişkin en temel cebirsel ifadeden türetilir. Örneğin, gelecekteki değer toplamı

Paranın zaman değerine dayalı bazı standart hesaplamalar şunlardır:
Bugünkü değer: Belirli bir getiri oranı göz önüne alındığında, gelecekteki bir para toplamının veya nakit akışı akışının bugünkü değeri. Gelecekteki nakit akışları iskonto oranı üzerinden “indirgenir”; iskonto oranı ne kadar yüksekse gelecekteki nakit akışlarının bugünkü değeri o kadar düşük olur. Uygun iskonto oranını belirlemek, ister kazanç ister yükümlülük olsun, gelecekteki nakit akışlarını doğru bir şekilde değerlemenin anahtarıdır.
Bir anüitenin bugünkü değeri: Anüite, eşit aralıklarla gerçekleşen bir dizi eşit ödeme veya gelirdir. Finansal kiralamalar ve kira ödemeleri buna örnektir. Ödemeler veya makbuzlar, normal bir anüite için her dönemin sonunda gerçekleşirken, vadesi gelen bir anüite için her dönemin başında gerçekleşir. Sürekli bir nakit akışının bugünkü değeri, özdeş nakit akışlarının sonsuz ve sabit bir akışıdır.
Gelecekteki değer: Bir varlığın veya nakdin gelecekte belirli bir tarihteki değeri, o varlığın bugünkü değerine dayanır.
Bir yıllık gelirin gelecekteki değeri (FVA): Ödemelerin belirli bir faiz oranında yatırıldığı varsayıldığında, bir ödeme akışının (yıllık gelir) gelecekteki değeri.
Dönem Sonu Konvansiyonu
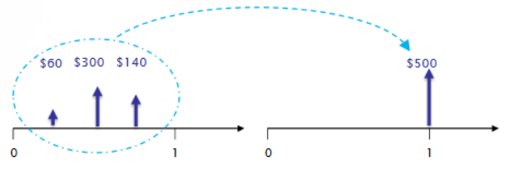
Pratikte, nakit akışları bir faiz döneminin başında veya ortasında ya da aslında zamanın herhangi bir noktasında gerçekleşebilir. Analizlerimizde kullandığımız basitleştirici varsayımlardan biri de dönem sonu kuralıdır. Dönem sonu kuralı:Aksi belirtilmedikçe, tüm nakit akışı işlemleri bir faiz döneminin sonunda gerçekleşir.
Faiz Hesaplama Yöntemleri
Basit faiz: sadece başlangıç tutarına (anapara) faiz oranı uygulanmasıdır.
Bileşik faiz: bir faiz oranının bir başlangıç tutarına ve daha önce birikmiş ve çekilmemiş olan herhangi bir faize uygulanmasıdır.
F= P+ (iP).N
P= Anapara
i= Basit faiz oranı
N= Periyot sayısı
F= N dönem sonunda biriken toplam miktar
Yıllık %33 basit faizle bankaya yatırılan 30.000 TL 5. ayın sonunda ne kadar olur?
Peki aynı miktar para birleşik faizle yatırılmış olsaydı?

2023 yılında hisse başına 0,40 USD’den halka arz olan bir şirketin 10 yıl boyunca dolar bazında yıllık birleşik büyüme oranının (CAGR) %16 olduğu var sayıldığında 10. yılın sonundaki değeri ne olacaktır?
F= 0,40 * (1+0,16) üzeri 10
F= 0,40* 4.4114350786499
= 1,764
1626 yılında Kızılderililer Manhattan Adası’nı Hollanda Batı Şirketi’nden Peter Minuit’e 24 dolara satmışlardır. Elde ettikleri gelirden sadece 1 doları %8 faiz ödeyen bir banka hesabında biriktirselerdi, torunlarının şu anda ne kadar parası olurdu?
2023 yılı itibariyle toplam ABD nüfusu 332 milyona yakın olurdu. Eğer toplam miktar nüfus arasında eşit olarak dağıtılsaydı, her bir kişi ne kadar alırdı?
P = $1 i = 8% N = 397 yıl
F = $1 (1+0.08)üzeri397 = $ 18,587,925,720,487
18,587,925,720,487/323,000,000 = 57457,76 USD
Yüzde 10 faiz ödeyen bir tasarruf hesabına şimdi 100 dolar (n = 0) ve iki yıl sonra 200 dolar (n = 2) yatırırsanız, 10. yılın sonunda ne kadar paranız olur?
Net Bugünkü Değer
Bugünkü değerin hesaplanması (iskonto), gelecekteki değerin hesaplanmasının (bileşik) tersidir:



Annüitenin Bugünkü Değeri
Önümüzdeki 3 yıl boyunca her yılın sonunda 100 $ getiri sağlayacak bir projeye yatırım yapabileceğinizi varsayalım. Yatırımınızdan yıllık %8 getiri oranı elde etmek istediğinize göre, bugün ne kadar yatırım yapmaya istekli olmalısınız?
T0 T1 T2 T3
$100 $100 $100
1 yıl geriye iskonto:
$100[1/(1.08)1] = $92.59
2 yıl geriye iskonto:
$100[1/(1.08)2] = $85.73
3 yıl geriye iskonto:
$100[1/(1.08)3] = $79.38
Bugünkü Değer = $257.70
Gelecek yılın sonunda başlamak üzere 20 eşit yıllık ödeme şeklinde ödenmek üzere 10.000.000$ tutarında bir devlet piyangosu kazandığınızı varsayalım. İskonto oranı %9 ise bu anüitenin bugünkü değeri (vergiler göz ardı edilerek) nedir?
P= 500.000* (((1-1/5,6044107))/0,09)))= 4.564.272,82255

Sebastian bir MacBook için satıcıyla görüştü. Satıcı yıllık %8 sabit faiz üzerinden hesaplama yaptığını belirterek 6 yıl boyunca her yıl dönem sonu 5.000TL ödeme yapmak şartıyla bilgisayarı satabileceğini belirtti. Sebastian bu hesaplamalara göre bilgisayarı peşin almak isterse ne kadar ödemelidir?
İlk olarak satıcı 5.000TL x 6 = 30.000TL fiyat istemiştir. Tabi ki bu hesaplamaları yaparken düzenli ödemelere %8 faiz eklemiştir. Bu satıcının taksitli ödeme fiyatıdır.
5.000 x ( ((1+0.08)^6 – 1) / (((1+0.08)^6) x 0.08 ) ) = 23.114,39TL
Sonuç olarak satıcı bu fiyat üzerinden bize ödeme planı çıkarmıştır. Bilgisayarın bugünkü değeri 23.114,39TL’dir.
