İstatistik belirli bir amaç için veri toplama, tablo ve grafiklerle özetleme, sonuçları yorumlama, sonuçların güven derecelerini açıklama, örneklerden elde edilen sonuçları kitle için genelleme, özellikler arasındaki ilişkiyi araştırma, çeşitli konularda geleceğe ilişkin tahmin yapma, deney düzenleme ve gözlem ilkelerini kapsayan bir bilimdir.
Belirli bir amaç için verilerin toplanması, sınıflandırılması, çözümlenmesi ve sonuçlarının yorumlanması esasına dayanır.
İstatistik 2’ye ayrılabilir:
1.Betimsel İstatistik (deskriptif, tanımlayıcı) : Betimsel istatistik, örneklemi sayısal veya grafiksel olarak özetlemek amacıyla kullanılabilir. Sayısal göstergelere temel örnek olarak ortalama ve standart sapma gösterilebilir. Grafiksel özetler çeşitli türde grafik ve tabloları içerir.
• Frekans dağılımı,
•Yer ölçüleri(aritmetik ortalama, geometrik ortalama, harmonik ortalama, kareli ortalama, mod ve medyan)
•Dağılma ölçüleri (ortalama, sapma, standart sapma, varyans gibi)
•Çarpıklık ve basıklık ölçüleri
2. Çıkarımsal İstatistik (indaktif, yorumlayıcı):
Çıkarımsal istatistik verideki örtüşmeleri modellemek için kullanılır, olasılığı göze alır ve daha büyük bir istatistiksel yığın hakkında sonuç çıkarır.
Bu sonuçlar, evet/hayır şeklinde cevaplar olabileceği gibi (hipotez testi), sayısal özelliklerin tahmin edilmesi (istatistiksel tahmin) gelecekteki değerlerin öngörülmesi (istatistiksel öngörü), veriler arasındaki doğrusal ilişkinin yorumlanması (korelasyon), veya bu ilişkilerin modellenmesi (regresyon analizi) şeklinde olur. Diğer belli başlı matematiksel modelleme teknikleri, varyans analizi, ANOVA, zaman serisi ve veri madenciliğidir.
Örnekleme Teorisi
Hipotez testleri
Regresyon ve Korelasyon analizi
Tanımlayıcı istatistik, verileri anlamlı bir şekilde tanımlamaya, göstermeye ve özetlemeye yardımcı olan verilerin analizine verilen bir terimdir. Verilerimizi tanımlamanın basit bir yoludur. Tanımlayıcı istatistikler, ham verilerimizi sayısal hesaplamalar veya grafikler veya tablolar kullanarak etkisiz/anlamlı bir şekilde sunmak için çok önemlidir. Bu tür istatistikler zaten bilinen verilere uygulanır.
Ana kütle kolektif olay özelliğinde ve aynı cinsten (homojen) birimlerin meydana getirdiği topluluktur. Birimler tamamen aynı özelliklere sahip olmasalar da , bazı ortak yanlarının bulunması gereklidir.
Bir ülkenin nüfusu, bir şehirdeki binalar belirli kütle, bir nehirdeki balıklar, ormandaki karıncalar sayılamayacağı için belirsiz kütledir.
•İstatistikte, popülasyon, bazı sorular veya deneyler için ilgi çekici olan benzer öğeler veya olaylar kümesidir. İstatistiksel bir popülasyon, var olan bir nesne grubu (örneğin, Samanyolu galaksisindeki tüm yıldızların kümesi) veya varsayımsal bir nesne grubu (örneğin, bir poker oyunundaki tüm olası ellerin kümesi) olabilir. İstatistiksel analizin ortak bir amacı, seçilmiş bazı popülasyonlar hakkında bilgi üretmektir.
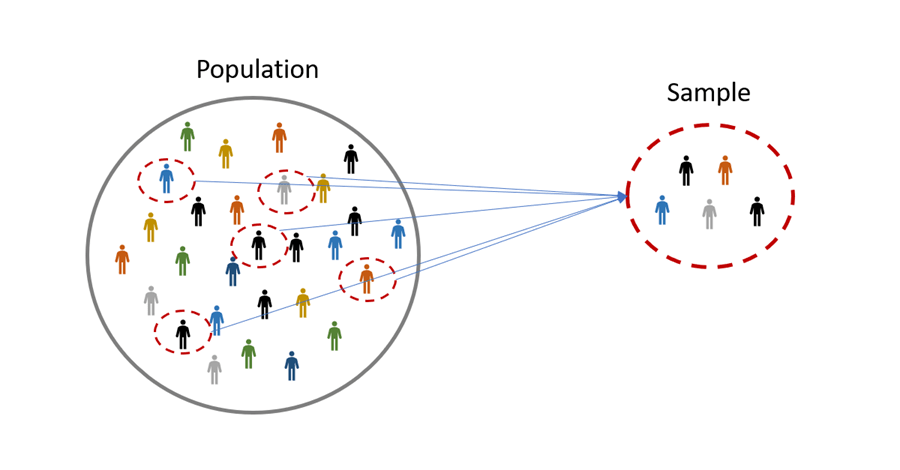
Örneklem, tanımlanmış bir prosedürle bir popülasyondan toplanan ve/veya seçilen bir veri setidir.
İstatistik kelimesi Modern Latincedeki statisticum collegium (devlet konseyi) ve İtalyancadaki statista (devlet adamı, politikacı) kelimelerinden türemiştir. Kelime ilk olarak Almanca’da Gottfried Achenwall tarafından devlete ait verilerin sunulduğu Statistik (1749) adlı eserde devlet bilimi anlamında kullanılmıştır.
Bu tanımı içeren İngilizce terim ise o dönemde political arithmetic (siyasi aritmetik) olarak geçmekteydi. İstatistik kelimesi veri toplama ve sınıflandırma anlamını ise yaklaşık olarak 19. yüzyılın başlarında kazanmıştır. Terim İngilizce’ye Sir John Sinclair tarafından aktarıldı. Statistik adlı eserin temel amacı hükümet tarafından ve yönetimsel organlar tarafından kullanılacak veriler sunmaktır.
İslam’ın Altın Çağı (VIII. –XIII. yy.)
el-Ferahidî: Al-Farahidi’nin “Kriptografik Mesajlar Kitabı”, bir dilbilimci tarafından yazılmış kriptografi ve kriptanaliz üzerine ilk kitaptı. Kayıp eser, ünlülü ve sesli tüm Arapça kelimeleri listelemek için permütasyonların ve kombinasyonların kullanımı da dahil olmak üzere birçok “ilk” içermektedir.
Kindî (Alkindus)(801-873): Frekans Analizi
«Şifreli bir mesajı çözmenin bir yolu, eğer onun dilini biliyorsak, aynı dilden bir veya daha fazla sayfayı dolduracak kadar uzun farklı bir düz metin bulmak ve sonra her harfin oluşumunu saymaktır. Düz metin örneğindeki tüm farklı harfleri hesaba katana kadar en sık geçen harfe “birinci”, bir sonraki en çok geçen harfe “ikinci”, ardından en çok geçen harfe “üçüncü” vb. diyoruz. Daha sonra çözmek istediğimiz şifreli metne bakarız ve sembollerini de sınıflandırırız. En çok meydana gelen sembolü buluyoruz ve onu düz metin örneğinin “birinci” harfinin biçimine değiştiriyoruz……….»
Ibn ‘Adlan: Örneklem Büyüklüğü
İbn ‘Adlan, Arapça cümlelerde her bir harfin ardışık olarak kaç kez geçebileceğini ve bunun gerçekleşmesinin belirli yollarını bilmeye dayalı ardışık harflerin analizinin yanı sıra frekans (sıklık) analizinin kullanılmasını tavsiye etti. Ayrıca boşluğun değişken sembollerle temsil edildiği şifrelerin analizi üzerine de yazdı.
İbn ‘Adlan, Arap alfabesini bölümlere ayırmıştır. yedi ortak (sıklıkla görülen), on bir orta ve on nadir harf. İbn ‘Adlan en yaygın iki veya üç harfli kelimelerin bir tablosunu sunar ve minimum bir örneklem boyutu, harf sıklığı kullanılarak kriptanaliz yapılabilen bir metin uzunluğu alt limiti sunar: yaklaşık 90 karakter (Arap alfabesinde bulunan harf sayısının yaklaşık üç katı).Bu sınırın altında, İbn Adlan’a göre harflerin oluşumu, sağlanan sıklık dağılımını takip etmeyecektir.
İstatistiğin konusu olan olaylar çoğu kez seçkisiz (tesadüfî) etmenlere bağlı olduğundan ,bu gibi etmenlerin gözlemler üzerindeki etkisi anlaşılmadan bilim gereğince gelişemez, istatistiksel çıkarımlarda geçerli genellemeler yapılamazdı. Bu bakımdan, seçkisizlik (rassallık/tesadüfilik) ilkelerini inceleyen olasılık hesaplama kuramlarında sağlanan gelişmeler istatistiğin evriminde önemli rol oynamıştır.
Olasılık konusundaki çalışmaların oldukça eski bir geçmişi vardır. Bu konuda düzenli çalışmalar, İtalyan bilimciler Pacioli (1445-1514) ve Cardano’nun (1501-1576) zar atma ve öbür şans oyunları hakkındaki yazıları ile başlamış sayılabilir.
İstatistiğin doğuşu genellikle, John Graunt’un William Petty ile birlikte modern demografi için bir çerçeve sağlayan erken insan istatistiksel ve nüfus sayımı yöntemlerini geliştirdiği 1662 yılına tarihlenir. Graunt, her yaşa hayatta kalma olasılıklarını veren ilk yaşam tablosunu üretti.
Doğal ve Politik Gözlemler Üzerine Yapılan Ölüm Bildirgeleri adlı kitabı, Londra nüfusunun ilk istatistiksel temelli tahminini yapmak için ölüm oranlarının analizini kullandı. Londra’da yılda yaklaşık 13.000 cenaze olduğunu ve yılda on bir aileden üç kişinin öldüğünü biliyordu. Kilise kayıtlarından ortalama aile büyüklüğünün 8 olduğunu tahmin etti ve Londra nüfusunun yaklaşık 384.000 olduğunu hesapladı; bu, bir oran tahmin edicisinin (ratio estimator) bilinen ilk kullanımıdır.
İstatistiğin matematiksel temelleri Pierre Fermat ve Blaise Pascal’ın 1654 yılına kadar giden olasılık kuramı hakkındaki yazışmalarına dayanır.
Sorun, her turda eşit kazanma şansına sahip iki oyuncu ile bir şans oyunu ile ilgilidir. Oyuncular bir ödül potuna eşit şekilde katkıda bulunur ve belirli sayıda tur kazanan ilk oyuncunun tüm ödülü alacağını önceden kabul eder. Şimdi varsayalım ki, her iki oyuncu da zafer kazanmadan önce oyun dış şartlar tarafından kesintiye uğrar. O zaman pot nasıl adil bir şekilde bölünür? Bölünmenin bir şekilde her oyuncunun kazandığı raunt sayısına bağlı olması gerektiği anlaşılmaktadır, böylece kazanmaya yakın olan bir oyuncu potun daha büyük bir bölümünü alacaktır.
Christiaan Huygens (1657) konunun bilinen ilk bilimsel uygulamasını sunmuştur. Galileo Galilei ve Rene Descartes ile arkadaş olduğu bilinmektedir.
Jakob Bernoulli’nin Ars Conjectandi (Tahmin Sanatı)(1713) ve Abraham de Moivre’nin Doctrine of Chances (1718) adlı eserleri konuya matematiğin bir dalı olarak yaklaşmıştır.
Pierre-Simon Laplace (1774), olasılıklar teorisinin ilkelerinden gözlemlerin birleşimi için bir kural çıkarmaya yönelik ilk girişimi yaptı. Hata olasılığı yasasını bir eğri ile temsil etti ve üç gözlemin ortalaması için bir formül çıkardı.
1774’te Laplace, bir hatanın sıklığının, işareti göz ardı edildiğinde, büyüklüğünün üstel bir fonksiyonu olarak ifade edilebileceğini kaydetti. Bu dağılım şimdi Laplace dağılımı olarak bilinir.
1786’da William Playfair (1759-1823), grafiksel temsil fikrini istatistiklere soktu. Çizgi grafiği, çubuk grafiği ve histogramı icat etti ve bunları ekonomi, Ticari ve Politik Atlas ile ilgili çalışmalarına dahil etti. Bunu 1795’te İngiltere’nin ithalat ve ihracatının gelişimini göstermek için kullandığı pasta grafiği ve daire grafiğini icat etmesi izledi. Bu son çizelgeler, 1801’de İstatistik Özeti’nde örnekler yayınladığında genel dikkatleri üzerine çekti.
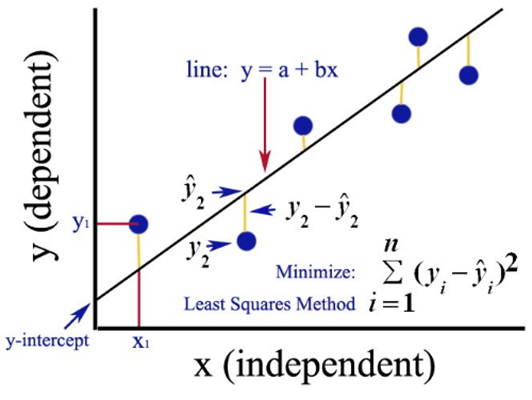
Veri ölçümündeki hataları en aza indirmek için kullanılan en küçük kareler yöntemi, Adrien-Marie Legendre (1805), Robert Adrain (1808) ve Carl Friedrich Gauss (1809) tarafından bağımsız olarak yayınlandı. Gauss, bu yöntemi, cüce gezegen Ceres’in konumuyla ilgili ünlü 1801 tahmininde kullanmıştı. Gauss’un hesaplamalarını temel aldığı gözlemler, İtalyan keşiş Piazzi tarafından yapılmıştır.
İstatistiğin bir diğer önemli kurucusu olan Adolphe Quetelet (1796-1874), suç oranları, evlilik oranları ve intihar oranları gibi karmaşık sosyal fenomenleri anlamanın bir yolu olarak “ortalama insan” (l’homme moyen) kavramını ortaya attı.
Normal dağılımın ilk testleri, 1870’lerde Alman istatistikçi Wilhelm Lexis tarafından icat edildi. Gösterebildiği tek normal dağılıma sahip olan veri seti, doğum oranlarıydı.
İstatistik teorisinin kökenleri 18. yüzyılda olasılıktaki gelişmelere dayansa da, modern istatistik alanı ancak 19. yüzyılın sonlarında ve 20. yüzyılın başlarında üç aşamada ortaya çıktı. İlk dalga, yüzyılın başında, istatistikleri sadece bilimde değil, endüstri ve siyasette de analiz için kullanılan titiz bir matematiksel disipline dönüştüren Francis Galton ve Karl Pearson’ın çalışmaları tarafından yönetildi.
1910’ların ve 20’lerin ikinci dalgası William Sealy Gosset tarafından başlatıldı ve doruk noktasına Ronald Fisher’ın içgörülerinde ulaştı. Bu, daha iyi deney modelleri tasarımının, hipotez testinin ve küçük veri örnekleriyle kullanım için tekniklerin geliştirilmesini içeriyordu. Esas olarak önceki gelişmelerin iyileştirilmesini ve genişletilmesini gören son dalga, 1930’larda Egon Pearson ve Jerzy Neyman arasındaki ortak çalışmadan ortaya çıktı.
Francis Galton, istatistiksel teorinin başlıca kurucularından biri olarak kabul edilir. Alana katkıları, standart sapma, korelasyon, regresyon kavramlarını tanıtmayı ve bu yöntemlerin çeşitli insan özelliklerinin – diğerleri arasında boy, kilo, kirpik uzunluğu – araştırılmasına uygulanmasını içeriyordu. Bunların birçoğunun normal bir eğri dağılımına uydurulabileceğini buldu.
Galton, 1907’de Nature’a medyanın kullanışlılığı hakkında bir makale sundu. Bir ülke fuarında bir öküzün ağırlığının 787 tahmininin doğruluğunu inceledi. Gerçek ağırlık 1208 pounddu: medyan tahmin 1198’di.
Galton’un 1889’da Natural Inheritance’ı yayınlaması, o sıralar University College London’da çalışan parlak bir matematikçi olan Karl Pearson’ın ilgisini çekti.
Onun ve Galton’ın çalışması, bugün yaygın olarak kullanılan birçok ‘klasik’ istatistiksel yöntemin temelini oluşturur; buna, bir çarpım-moment olarak tanımlanan Korelasyon katsayısı; dağılımların örneklere uydurulması için momentler yöntemi de dahildir. Ayrıca ‘standart sapma’ terimini de tanıttı.
Ayrıca istatistiksel hipotez testi teorisini, Pearson’ın ki-kare testi ve temel bileşen analizini kurdu. 1911’de University College London’da dünyanın ilk üniversite istatistik bölümünü kurdu.
BÜYÜK SAYILAR KANUNU
Büyük sayılar kanunu ilk olarak Jacob Bernoulli tarafından tanımlanmıştır. 1713’te Ars Conjectandi (Tahmin Sanatı) adlı eserinde yayınlanan yeterli derecede titiz bir kanıtı geliştirebilmesi 20 yılına mal olmuştur. Bunu kendisinin “Altın Teoremi” olarak adlandırmış, fakat yaygın olarak “Bernoulli’nin Kuramı” olarak bilinmektedir
1835’te S.D. Poisson, bu yasayı “La loi des grands nombres” (Büyük sayılar yasası) olarak adlandırmıştır . İki isimde de anılagelen bu yasa için “Büyük sayılar yasası” terimi daha fazla kullanılmaktadır.
Büyük sayılar yasası bir rassal değişkenin uzun vadeli kararlılığını tanımlayan bir olasılık teoremidir. Sonlu bir beklenen değere sahip birbirinden bağımsız ve eşit dağılıma sahip bir rassal değişkenler örneklemi verildiğinde, bu gözlemlerin ortalaması sonuçta bu beklenen değere yakınsayacak ve bu değere yakın bir seyir izleyecektir.
Büyük sayılar yasası bir zarın peş peşe atılması ile örneklenebilir. Öyle ki, multinom dağılımı sonucunda 1, 2, 3, 4, 5 ve 6 sayılarının gelme olasılığı eşittir. Bu sonuçların nüfus ortalaması (ya da “beklenen değeri),
(1 + 2 + 3 + 4 + 5 + 6) / 6 = 3,5 olur.
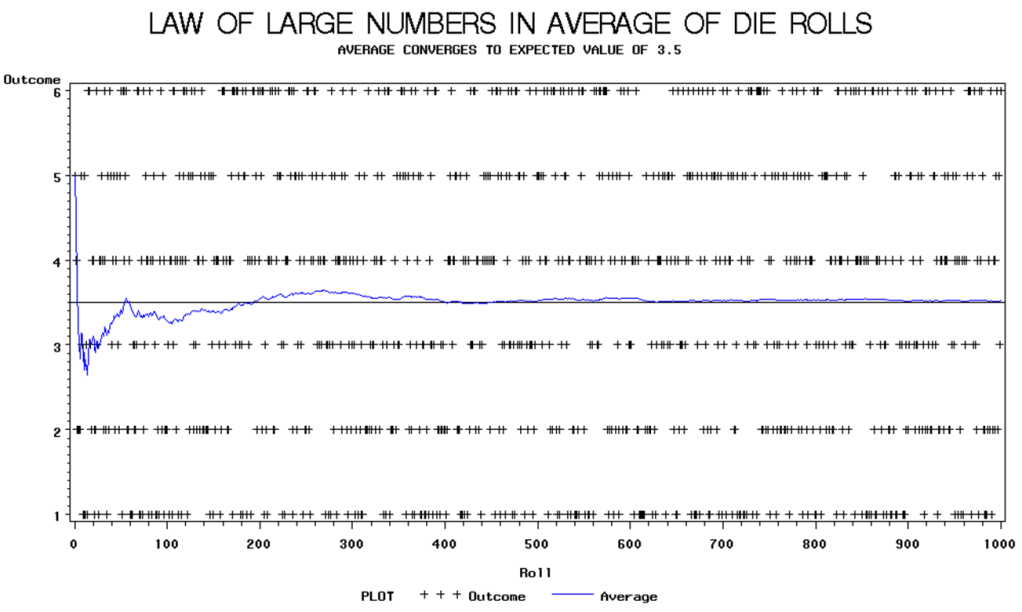
Bir başka örnek madeni para atılması olabilir. Bir madeni paranın peş peşe atılması durumunda, yazıların (ya da turaların) sıklığı, gözlem sayısı arttıkça, %50’e gittikçe yaklaşacaktır. Fakat yazı ve tura sayıları arasındaki mutlak fark atış sayısı arttıkça açılacaktır.
İSTATİSTİĞİN EKONOMİ İLE İLGİSİ
Şu bir gerçektir ki, ekonomi ilkelerinin anlaşılmasında en önemli unsur, mantığa dayanan yorumdur. Ekonomik etkinliklerin algılanmasında ise, en önemli unsur, ampirik kanıtların özenle incelenmesidir.
Ekonomi bir bakıma kantitatif (nicel) olaylarla uğraştığı için matematik, geometri ve olasılık hesaplarından büyük ölçüde yararlanır. Ekonomik olayların nicel ilişkilerin araştırılmasında matematiksel yöntemlerden yararlanılmaktadır. Örneğin fiyatlar, maliyetler, gelir, kar ve zarar gibi unsurlar, sayılarla ifade edildiklerinden, bunların araştırılması ve incelenmesinde matematiksel çözümlemelere gerek duyulur.
$1.00’lık bir banka hesabı yıllık yüzde 100 faiz ile açılıyor. Eğer faiz, yılsonunda, bir kere uygulanırsa para $2.00 olmaktadır. Ancak eğer faiz hesaplanıp yılda iki kez uygulanırsa (yüzde 50 olarak iki kez), $1.00 1.5 ile iki kez çarpılır, elde edilecek para $1.00×1.5² = $2.25 olur. Bu işlem herhangi bir n sayısı kez tekrarlanırsa getirinin limiti nerede oluşur?
Kaynakça
https://tr.wikipedia.org/wiki/%C4%B0statistik
http://web.itu.edu.tr/~seker/files/Istatistik.html
http://ilker.utlu.net/blog/buyuk-sayilar-yasasi/
https://tr.wikipedia.org/wiki/B%C3%BCy%C3%BCk_say%C4%B1lar_yasas%C4%B1
Çil, Burhan. (2013). İstatistik. Ankara: Detay Yayıncılık
Yüzer, A. F., Ağaoğlu, E., vd. (2003). İstatistik. Eskişehir: Anadolu Üniversitesi Yayınları
