Öncelikle terimsel bir ifadenin anlam karmaşasını çözerek yazıya başlamak yerinde olacaktır. Seri ya da dizi bir sekanstaki sayıların toplamını ifade ederken, sekans ise art arda gelen sayılar anlamındadır. Bu ifadelerin birbiri yerine kullanılması oldukça rastlanan bir durum olduğundan meseleye açıklık getirmek yazının geri kalanının da daha iyi anlaşılması için önemliydi. Hoşuma giden serilerin bir kısmını aşağıda bulabilirsiniz.
Fibonacci Sayıları (Sekansı)
Fibonacci Sekansı, birbirini takip eden her sayının dizideki önceki iki sayının toplamı olduğu matematiksel bir sekanstır. Şu şekilde gösterilebilir
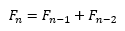
Bu seri 0,1 şeklinde başlamaktadır. Bu denklem kullanılarak, dizideki ilk 12 sayı aşağıdaki gibi belirlenebilir
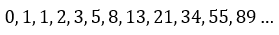
Bu dizi dünya çapında en iyi bilinen dizilerden biridir ve çeşitli çevresel ortamlarda görülebilir. Bu örneklerden biri, ayçiçeği tohumlarının sayıldığında Fibonacci sekansıyla sonuçlanacak olan spiral oluşumunu içerir. Bir başka örnek de sukulentler gibi bazı bitkilerin yaprak düzenlemelerinde görülebilir.

Dizinin kullanımı, veriler arasında arama yaparken ve grafikler oluştururken kullanılan bilgisayar algoritmaları gibi alanlara da uygulanabilir. Fibonacci sekansı bir yineleme dizisidir, yani sonraki terimler dizideki önceki terimler kullanılarak belirlenebilir. Bu nedenle Fibonacci sekansı, önceki terimler sürekli olarak yeni terimler bulmak için kullanılabildiğinden sonsuz bir sekansdır
Adını, Fibonacci olarak da bilinen ve 1202 yılında Liber Abaci adlı kitabında bu sekansı Batı Avrupa matematiğine kazandıran İtalyan matematikçi Pisa’lı Leonardo’dan almıştır.
Fibonacci sayıları matematikte beklenmedik bir şekilde sıkça karşımıza çıkmaktadır, öyle ki Fibonacci Quarterly adında bu sayıların incelenmesine adanmış bir dergi bulunmaktadır. Fibonacci sayılarının uygulamaları arasında Fibonacci arama tekniği ve Fibonacci yığın veri yapısı gibi bilgisayar algoritmaları ve paralel ve dağıtık sistemleri birbirine bağlamak için kullanılan Fibonacci küpleri adı verilen grafikler yer almaktadır. Tüm türlerde görülmese de, ağaçlardaki dallanma, yaprakların bir gövde üzerindeki dizilimi, ananasın meyve filizleri, enginarın çiçeklenmesi ve çam kozalağının brakte dizilimi gibi biyolojik ortamlarda da görülürler.
Fibonacci sayıları da altın oranla güçlü bir şekilde ilişkilidir: Binet’in formülü n’inci Fibonacci sayısını n ve altın oran cinsinden ifade eder ve ardışık iki Fibonacci sayısının oranının n arttıkça altın orana doğru eğilim gösterdiğini ima eder. Fibonacci sayıları, aynı yineleme ilişkisine uyan ve Fibonacci sayılarıyla birlikte Lucas sekanslarının tamamlayıcı bir çiftini oluşturan Lucas sayılarıyla da yakından ilişkilidir.
Sabit katsayılı doğrusal bir yineleme ile tanımlanan her sekans gibi, Fibonacci sayılarının da kapalı formda bir ifadesi vardır. Abraham de Moivre ve Daniel Bernoulli tarafından zaten bilinmesine rağmen, adını Fransız matematikçi Jacques Philippe Marie Binet’den alan Binet formülü olarak bilinir hale gelmiştir:
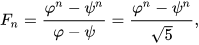
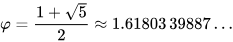

Phi ile ifade edilen sayının altın oran olduğunu hatırlayalım. Altın oran a ve b’nin 0’dan büyük olması durumunda (a+b)/a=a/b eşitliğinden çıkarılabilir.
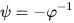
olduğu için bu formül şu şekilde de yazılabilir:
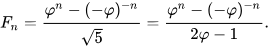
Lucas Sayıları (Sekansı)
Lucas sayıları Fibonacci sayılarına çok benzer. Her ikisi de sekanstaki bir sonraki sayıyı elde etmek için önceki iki sayının toplamını aldığınız aynı modeli izler. Burada farklı oldukları nokta başlangıç değerleridir. Lucas sekansının başlangıç değerleri, ilk iki Fibonacci sayısı F0 = 0 ve F1 = 1’in aksine L0 = 2 ve L1 = 1’dir. Aşağıda Lucas sekansının ilk 12 değerini göreceksiniz.
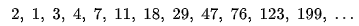
Hem Fibonacci sayıları hem de Lucas sayıları Lucas dizilerinin tamamlayıcı örneklerini oluşturduğundan, birbirleriyle bazı ilişkileri paylaşırlar. Bu ilişkilerden biri, Fibonacci dizisi üzerinde iki terim arayla herhangi iki değeri topladığınızda, aralarındaki Lucas dizisi numarasını elde edeceğinizdir.
Bu ilişkilerden bir diğeri de her ikisinin de özyinelemeli olmasıdır, yani bir sonraki terim dizi içinde daha önce bilinen terimler kullanılarak bulunabilir. Lucas sayılarını belirlerken, birbirleriyle ne kadar yakından ilişkili oldukları için aşağıdaki denklemi kullanarak Fibonacci dizisi içindeki terimleri kullanabilirsiniz.
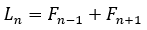
Örneğin Lucas sekansı 11. sayıyı arıyorsak Fibonacci sekansındaki 10. ve 12. sayıyı toplamamız yeterli olacaktır. Buradaki formülde yerine koyduğumuzda; 123= 34+89 sonucuna ulaşırız.
Tembel Aşçının Sekansı
Tembel Aşçı sekansı, disk şeklindeki bir nesnenin belirli sayıda düz kesimle kesilebileceği maksimum parça miktarını tanımlar. Örneğin, ortada birleşen 3 dilim kullanılarak eşit şekilde kesilen bir daire 6 parça oluşturacaktır. Ancak, kesikler ortada birleştirilmemiş ve bunun yerine düzensiz kesilmişse, bunun yerine 7 parça olacaktır.
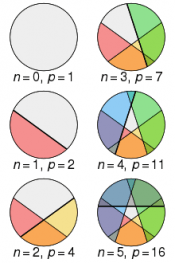
Daha resmi olarak merkezi poligonal sayılar olarak bilinir.
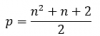
Merkezi poligonal sayılar bu dizide temsil edilir:
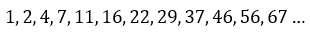
Eğer tanıdık geliyorlarsa, bunun nedeni her sayının üçgen sayılar sekansındaki karşılık gelen terimle aynı olması ancak bir artırılmış olmasıdır.
Üçgen Sayılar Sekansı
Üçgen sayı sekansı, eşkenar üçgen şeklinde düzenlenebilen bir sayı sekansıdır. Dizinin bu özelliği nedeniyle, üçgen sayı dizisi, küp sayılar ve kare sayılar ile birlikte bir figüratif (bir şekle/görsele atfen) sayı olarak kabul edilir. Bu dizi sonsuz bir uzunluğa sahiptir ve sonsuza kadar büyüyebilir. Dizinin ilk 12 terimi aşağıdaki gibidir:
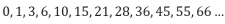
Seri için kullanılan formül aşağıdaki gibidir:
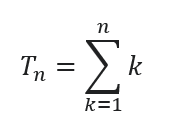
Burada Tn n’inci üçgen sayısını, n sekanstaki sırayı ve k pozitif bir tamsayıyı temsil eder. Ayrıca şu şekilde de ifade edilebilir:

Üçgen sayıların kare sayılarla da yakın bir ilişkisi vardır. Ardışık iki üçgen sayının toplamı, bir üçgenin alanının bir karenin alanının yarıya indirilmesiyle bulunabilmesine benzer şekilde bir kare sayıya eşittir.
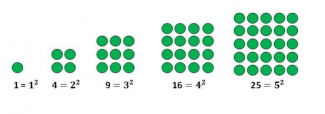
0+1=1 , 1+3=4, 3+6=9, 6+10=16, 10+15=25 vb.
“Bak ve Söyle” Sekansı
Bak ve söyle sekansı, terimlerin bulunma yöntemi nedeniyle benzersiz bir sekanstır. Sekansın elemanlarını belirlemek için, bir sonrakini bulmak üzere sekanstaki mevcut sayıya bakmak ve söylemek yeterlidir. İlk sekiz değer aşağıda gösterilmiştir.
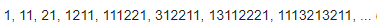
Bu değerleri belirlemek için aşağıdaki adımları takip etmek yeterlidir
- İlk değer sadece 1’dir
- İkinci değer için, 11’i elde etmek üzere “bir bir” gördüğünüz ilk değere bakarsınız
- Üçüncü değer için 11’e bakarsınız ve “iki bir” olarak okursunuz çünkü iki tane 1 vardır
- Dördüncü değer için 21’e bakarsınız ve “bir 2 bir 1” olarak okursunuz.
- Beşinci değer için 1211’e bakarsınız ve “bir 1, bir 2, iki 1” olarak okursunuz.
- Altıncı değer için 111221’e bakarsınız ve bunu “üç 1, iki 2, bir 1” olarak okursunuz.
Bu dizi sonsuza kadar büyüyecek ve 1, 2 veya 3 dışında bir rakam içermeyecektir.
Yellowstone Permütasyon Tamsayı Sekansı
Yellowstone permütasyonu: n <= 3 ise a(n) = n, aksi takdirde a(n-2) ile en az bir ortak çarpanı olan, ancak a(n-1) ile hiçbir ortak çarpanı olmayan daha önce ortaya çıkmayan en küçük sayı. Bu dizinin bu ismi almasının nedeni, permütasyonunun bir grafik üzerinde bakıldığında Yellowstone Ulusal Parkı’nda bulunan gayzerlere benzemesidir. Dahası, tüm sekans, sekanstaki tüm pozitif tam sayıların bir permütasyonudur. Ve bu da onu şaşırtıcı matematik sekanslarından biri yapan şeydir.
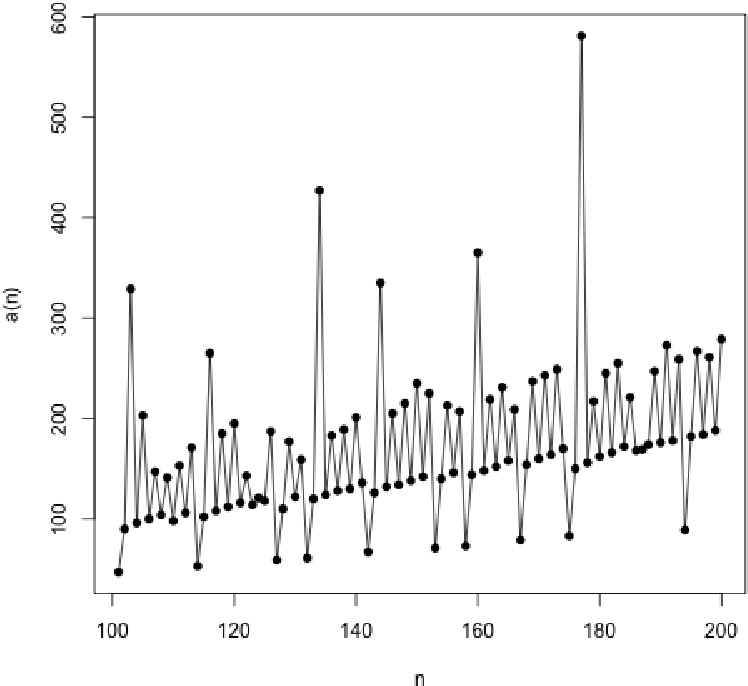
Yellowstone permütasyonunun a(101)’den a(200)’e kadar olan terimlerinin grafiği. Aşağı doğru sivri uçlar a(n) bir asal olduğunda meydana gelir ve daha büyük yukarı doğru sivri uçlar (“gayzerler”) iki adım sonra meydana gelir.
Yellowstone sekansı, sekanstaki dördüncü sayının 2 ile ortak bir çarpana sahip olması ancak 3 ile olmaması; beşinci sayının 3 ile ortak bir çarpana sahip olması ancak 4 ile olmaması; ve altıncı sayının 4 ile ortak bir çarpana sahip olması ancak 9 ile olmaması kuralını izler: 1, 2, 3, 4, 9, 8, 15, 14, vb.
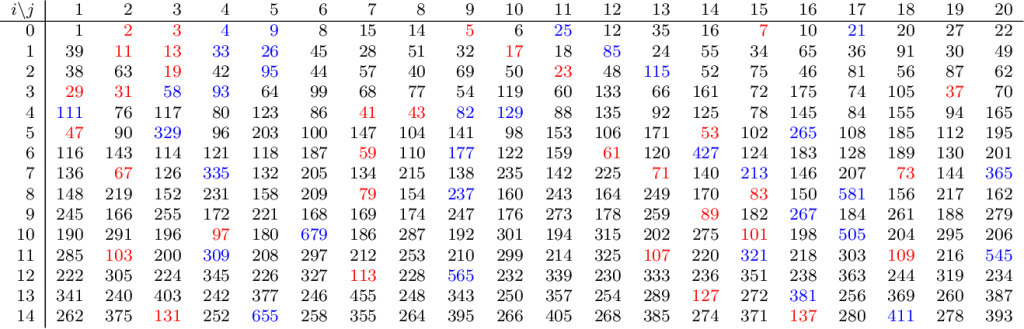
Yellowstone permütasyonunun ilk 300 terimi a(20i+j), 0 ≤ i ≤ 14, 1 ≤ j ≤ 20. Asal sayılar (veya aşağı doğru sivri uçlar) kırmızı, “κp” noktaları (yukarı doğru sivri uçlar veya “gayzerler”) mavi ile gösterilmiştir.
Padovan Sekansı ve Perrin Sekansı
Bu dizilerin her ikisi de “skiponacci” olarak adlandırılır çünkü dizideki bir sonraki sayının toplamı dizideki önceki iki sayının toplamıdır. Tek fark, Padovan dizisi 1, 1, 1 ile başlarken Perrin dizisinin 3, 0, 2 ile başlamasıdır.
Bir Padovan sekansı şöyle görünecektir: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37 ve bu şekilde devam eder.
Öte yandan Perrin sekansı şöyle görünecektir: 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, 119, 158 ve benzeri.
Bunları şaşırtıcı matematik sekansları yapan şey, her iki döngünün de sekanstaki 168. sayıdan sonra tekrar etmesi ve ardışık terimler arasındaki oranın plastik sabit adı verilen sınırlayıcı bir değere yaklaşmasıdır. Matematikte plastik sabit irrasyonel bir sayıdır ve x^3 – x – 1 = 0 kübik denkleminin gerçek değerli köküdür.
Bazen le nombre radiant, minimal Pisot sayısı, plastik sayı, plastik oran, platin sayısı, Siegel sayısı veya gümüş sayı olarak da adlandırılan plastik sabit P, Padovan sekansı veya Perrin sekansının ardışık terimlerinin sınırlayıcı oranıdır. Bu sayı şu şekilde verilir:
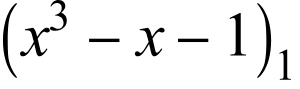
Eşittir;

O da eşittir;
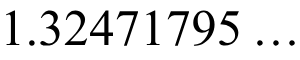
Recaman Sekansı
Matematik ve bilgisayar bilimlerinde, Recamán sekansı bir yineleme ilişkisi ile tanımlanan iyi bilinen bir sekanstır. Elemanları önceki elemanlarla basit bir şekilde ilişkili olduğundan, genellikle özyineleme kullanılarak tanımlanırlar. Adını Kolombiyalı bir matematikçi olan mucidi Bernardo Recamán Santos’tan alır.
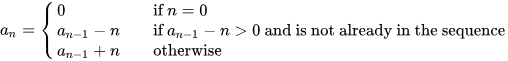
Dizinin ilk terimleri şunlardır:
0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, 77, 39, 78, 38, 79, 37, 80, 36, 81, 35, 82, 34, 83, 33, 84, 32, 85, 31, 86, 30, 87, 29, 88, 28, 89, 27, 90, 26, 91, 157, 224, 156, 225, 155, . ..
Catalan Sayıları (Sekansı)
Kombinatoryal matematikte Catalan sayıları, genellikle özyinelemeli olarak tanımlanmış nesneleri içeren çeşitli sayma problemlerinde ortaya çıkan bir dizi doğal sayıdır. Adlarını Fransız-Belçikalı matematikçi Eugène Charles Catalan’dan alırlar. n’inci Catalan sayısı doğrudan merkezi binom katsayıları cinsinden şu şekilde ifade edilebilir:
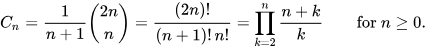
n = 0, 1, 2, 3, … için ilk Catalan sayıları şunlardır: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786,……
Kaynakça
https://idealminischool.ca/idealpedia/index.php/Other/Special_Sequences_and_Series
https://mathworld.wolfram.com/PlasticConstant.html
Applegate, D. L., Havermann, H., Selcoe, B., Shevelev, V., Sloane, N. J., & Zumkeller, R. (2015). The yellowstone permutation. arXiv preprint arXiv:1501.01669.
