Pergeli Apollonius

Pergeli Apollonius (Yunanca: Ἀπολλώνιος ὁ Περγαῖος ; yak. MÖ 240 – yak. MÖ 190) konik kesitler üzerine çalışmalarıyla tanınan eski bir Yunan coğrafyacı ve astronomdur. Öklid ve Arşimet’in konuyla ilgili daha önceki katkılarından yola çıkarak, onları analitik geometrinin icadından önceki duruma getirdi. Elips, parabol ve hiperbol terimleri için yaptığı tanımlar bugün kullanılan tanımlardır. Apollonius, selefleri Euclid ve Archimedes ile birlikte genellikle antik çağın en büyük matematikçileri arasında kabul edilir.

Apollonius geometrinin yanı sıra astronomi de dahil olmak üzere çok sayıda başka konu üzerinde de çalışmıştır. Bu çalışmaların çoğu günümüze ulaşmamıştır, istisnalar ise İskenderiyeli Pappus gibi başka yazarlar tarafından atıfta bulunulan parçalardır. Ortaçağ’a kadar yaygın olarak inanılan gezegenlerin görünüşteki sapkın hareketlerini açıklamak için kullandığı eksantrik yörüngeler hipotezi Rönesans döneminde geçersiz kılınmıştır. Ay’daki Apollonius krateri onun onuruna adlandırılmıştır.

Apollonius üretken bir coğrafyacıydı ve çok sayıda eser verdi. Günümüze sadece bir tanesi ulaşmıştır: Konikler. Sekiz kitabından sadece ilk dördü Apollonius’un çevrilmemiş orijinal metinleri olarak varlığını sürdürmektedir. 5-7. Kitaplar sadece Banû Mûsâ tarafından yaptırılan Sâbit ibn Kurra’nın Arapça çevirisinde mevcuttur; orijinal Yunanca kayıptır. Kitap 8’in durumu bilinmemektedir. Bir ilk taslağı mevcuttur, ancak son taslağının hazırlanıp hazırlanmadığı bilinmemektedir. Edmond Halley tarafından Latince bir “yeniden oluşturulması” mevcuttur, ancak bunun ne kadarının, eğer varsa, Apollonius’a benzediğini bilmenin bir yolu yoktur.

Konikler’in Yunanca metni tanımların, şekillerin ve bunların parçalarının Öklidyen düzenini kullanır; yani “verilenler “i “kanıtlanacak” önermeler takip eder. Kitap I-VII 387 önerme sunmaktadır. Bu tür bir düzenleme, geleneksel konuya ilişkin herhangi bir modern geometri ders kitabında görülebilir. Herhangi bir matematik dersinde olduğu gibi, malzeme çok yoğundur ve üzerinde düşünmek zorunlu olarak yavaştır. Apollonius’un her kitap için kısmen önsözlerde açıklanan bir planı vardı. Başlıklar ya da plana dair işaretler biraz eksiktir, Apollonius daha çok konuların mantıksal akışına bağlı kalmıştır.

Kitaplar hakkında yazılmış İngilizce metnin orijinaline ulaşmak için tıklayınız.

Kitap I

Kitap I 58 önerme sunmaktadır. En dikkat çekici içeriği koniler ve konik kesitlerle ilgili tüm temel tanımlardır. Bu tanımlar aynı kelimelerin modern tanımlarıyla tam olarak aynı değildir. Etimolojik olarak modern kelimeler antik kelimelerden türemiştir, ancak etimonu genellikle anlam olarak refleksinden farklıdır.

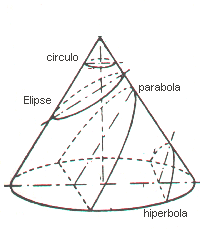
Konik bir yüzey, uç noktaları her biri kendi düzleminde daireler izleyecek şekilde bir açıortay noktası etrafında döndürülen bir doğru parçası tarafından oluşturulur. Çift konik yüzeyin bir kolu olan koni, noktası (tepe veya tepe noktası), dairesi (tabanı) ve ekseni, tepe noktası ile taban merkezini birleştiren bir doğrusu olan yüzeydir.

Bir kesit (Latince sectio, Yunanca tome), bir koninin bir düzlem tarafından hayali olarak “kesilmesidir”.

Kitap I Önsöz

” Apollonius’tan Eudemus’a, selamlar.
” Eğer sağlığınız yerindeyse ve diğer koşullar da istediğiniz gibiyse, sorun yok; ben de oldukça iyiyim. Bergama’da sizinle birlikteyken, konilerle ilgili çalışmalarım hakkında bilgi sahibi olmak için sabırsızlandığınızı gözlemledim; bu nedenle size İlk kitabı düzelttim ve diğer kitapları da bitirdiğimde memnuniyetimi bildireceğim. İskenderiye’ye gelip benim yanımda kaldığı sırada Nukrates’in isteği üzerine bu konuyu araştırmaya giriştiğimi ve sekiz kitap halinde hazırladıktan sonra, biraz da aceleyle, tam bir gözden geçirme yapmadan (çünkü denize açılmak üzereydi), ama aklıma gelen her şeyi, daha sonra yeniden ele almak niyetiyle, bir kerede kendisine ilettiğimi söylediğimi unutmamışsınızdır sanırım. Bu nedenle şimdi her bir bölümü zaman zaman düzeltilmiş olarak yayınlama fırsatını buluyorum. Ancak, benimle birlikte olan başka bazı kişiler de birinci ve ikinci kitapları düzeltilmeden önce almış olduklarından, onları farklı bir şekilde bulursanız şaşırmayın.”

” Bu sekiz kitaptan ilk dördü temel bir giriş niteliğindedir; ilki [hiperbolün] üç kesitini ve karşıt dallarını üretme biçimlerini ve bunların diğer yazarların yazılarında olduğundan daha tam ve genel olarak işlenmiş temel özelliklerini içerir; ikincisi kesitlerin çaplarının ve eksenlerinin özelliklerinin yanı sıra asimptotları ve genel öneme sahip ve olasılık sınırlarını belirlemek için gerekli olan diğer şeyleri ele alır ve çaplar ve eksenler ile neyi kastettiğimi bu kitaptan öğreneceksiniz. Üçüncü kitap, katı yerlerin sentezi ve sınırların belirlenmesi için yararlı birçok dikkate değer teorem içerir; bu teoremlerin çoğu ve en güzelleri yenidir ve onları keşfettiğimde, Öklid’in üç ve dört çizgiye göre yerlerin sentezini yapmadığını, sadece tesadüfi bir kısmını yaptığını ve bunun da başarılı olmadığını gözlemledim: çünkü sentezin benim ek keşiflerim olmadan tamamlanması mümkün değildi. Dördüncü kitap, konilerin kesitlerinin birbirleriyle ve bir çemberin çevresiyle kaç şekilde buluştuğunu gösterir: buna ek olarak, bir koninin kesitinin veya bir çemberin çevresinin [bir hiperbolün karşıt kollarıyla] buluştuğu noktaların sayısına ilişkin, daha önceki yazarlar tarafından hiçbiri tartışılmamış olan başka konuları da içerir*. “Geri kalan [kitaplar] daha çok fazlalık niteliğindedir: bunlardan biri minimumu ve maksimumu, biri konilerin eşit ve benzer kesitlerini, biri limitlerin belirlenmesini içeren teoremleri ve sonuncusu da belirli konik problemleri tam olarak ele almaktadır.”

” Tüm kitaplar yayınlandığında, onları okuyanlar elbette kendi istedikleri gibi değerlendirebileceklerdir. Elveda.”

Kitap II

Kitap II 53 önerme içermektedir. Apollonius, “çaplar ve eksenlerle ilgili özellikleri ve ayrıca asimptotları ve diğer şeyleri … olasılık sınırları için” kapsamayı amaçladığını söyler. Onun “çap” tanımı gelenekselden farklıdır, çünkü mektubun hedeflenen alıcısını bir tanım için kendi çalışmasına yönlendirmeyi gerekli bulmaktadır. Bahsedilen unsurlar, figürlerin şeklini ve oluşumunu belirleyen unsurlardır. Teğetler kitabın sonunda ele alınmaktadır.

Kitap II Önsöz

” Apoliouius’tan Eudenius’a, selamlaşma.
“Sağlığın yerindeyse, iyi; ben de orta derecede iyiyim. Oğlum Apollonius’u, topladığım conilerin ikinci kitabıyla birlikte sana gönderdim. Onu dikkatle inceleyin ve bu tür çalışmalara katılmaya layık olanlara iletin. Ve eğer sana tanıştırdığım geometrici Philonides Efes’te, herhangi bir zamanda çevreyi ziyaret ederse Bergama’dan, kitabı ona ilet. Sağlığınıza dikkat edin. Elveda.”

Kitap III

Kitap III 56 önerme içerir. Apollonius, “katı yerlerin inşasında kullanılan… üç çizgi ve dört çizgi yer ….” teoremleri için orijinal keşif iddiasında bulunur. Bir konik kesitin lokusu kesittir. Üç doğrulu konum problemi (Taliafero’nun Kitap III’ün ekinde belirttiği gibi) “verilen üç sabit doğruya olan uzaklıkları … uzaklıklardan birinin karesi her zaman diğer iki uzaklığın içerdiği dikdörtgene sabit bir oranda olacak şekilde olan noktaların konumunu” bulur. Bu, parabol ile sonuçlanan alan uygulamasının kanıtıdır. Dört çizgi problemi elips ve hiperbol ile sonuçlanır. Analitik geometri, Descartes’ın büyük övgüler aldığı geometriden ziyade cebirle desteklenen daha basit kriterlerden aynı konumları türetir. Yöntemlerinde Apollonius’un yerini alır.

Kitap IV

Kitap IV 57 önerme içerir. Eudemus’tan ziyade Attalus’a gönderilen ilk kitaptır ve bu nedenle onun daha olgun geometrik düşüncesini temsil eder. Konu oldukça özeldir: “Bir koninin kesitlerinin birbiriyle buluşabileceği ya da bir dairenin çevresiyle buluşabileceği en büyük nokta sayısı, ….” Yine de şevkle konuşur ve problemlerin çözümünde “önemli ölçüde işe yaradıklarını” belirtir.

Kitap IV Önsöz

” Apollonius’tan Attalus’a, selamlar.
” Bir süre önce Bergamalı Eudemus’a sekiz kitapta toplanan konilerimin ilk üç kitabını açıklamış ve göndermiştim; ancak o vefat ettiği için, eserlerime sahip olma konusundaki samimi arzunuzdan dolayı kalan kitapları size göndermeye karar verdim. Bu doğrultuda şimdi size dördüncü kitabı gönderiyorum. Bu kitapta, konilerin kesitlerinin birbirleriyle ve bir çemberin çevresiyle en fazla kaç noktada buluşmasının mümkün olduğu sorusu, bunların baştan sona çakışmadığı varsayımıyla, ve ayrıca bir koninin kesitinin ve bir çemberin çevresinin [bir hiperbolün] karşıt kollarıyla en fazla kaç noktada buluştuğu sorusu* ve bu soruların yanı sıra benzer nitelikte birkaç soru daha yer almaktadır. Conon, Thrasydaeus’a ilk soruyu açıklamış, ancak kanıtlar konusunda yeterli ustalığı gösterememişti; bu nedenle Kireneli Nikoteles bir nedenle ona ters düşmüştü. İkinci mesele sadece Nicoteles tarafından, Conon’a saldırısıyla bağlantılı olarak, kanıtlanabilecek bir mesele olarak bahsedilmiştir; ancak ne kendisi ne de başka biri tarafından bu şekilde kanıtlandığını görmedim. Üçüncü sorunun ve ona benzer diğer soruların hiç kimse tarafından fark edildiğini görmedim. Ve şimdiye kadar kanıtlanmış olarak bulamadığım tüm bu konular, pek çok ve çeşitli yeni teoremler gerektiriyordu; bunların çoğunu ilk üç kitapta zaten açıklamıştım, geri kalanı ise bu kitapta yer almaktadır. Bu teoremlerin araştırılması, hem problemlerin sentezi hem de problemlerin çözümü için büyük bir hizmettir.
olasılığın sınırları. Öte yandan Nicoteles, Conon’la olan tartışması nedeniyle, Conon’un keşiflerinden sınırların belirlenmesi için herhangi bir şekilde yararlanılabileceğini düşünmemektedir: bu görüşünde yanılmaktadır, çünkü onları hiç kullanmadan bu tür belirlemelerle ilgili sonuçlara ulaşmak mümkün olsa bile, yine de bazı şeyleri gözlemlemek için daha hazır bir araç sağlarlar, ör. Örneğin, birkaç çözümün mümkün olduğu ya da sayıca çok fazla oldukları ve yine hiçbir çözümün mümkün olmadığı gibi; ve bu tür önceki bilgiler araştırmalar için tatmin edici bir temel sağlarken, söz konusu teoremler sınırların belirlenmesinin analizi için daha da yararlıdır. Dahası, böyle bir yararlılığın yanı sıra, matematikteki diğer pek çok şeyi bu nedenle kabul ettiğimiz gibi, bu teoremler de kanıtların kendileri için kabul edilmeye değerdir.”

Kitap V

Sadece Arapçadan çeviri yoluyla bilinen V. Kitap 77 önerme içerir ki bu sayı tüm kitaplar arasında en fazladır. Bunlar elips (50 önerme), parabol (22) ve hiperbolü (28) kapsar. Bunlar, Önsöz I ve V’te Apollonius’un maksimum ve minimum çizgiler olduğunu belirttiği konu değildir. Bu terimler açıklanmamıştır. Kitap I’in aksine, Kitap V hiçbir tanım ve açıklama içermez.

Bu belirsizlik, kitabın ana terimlerinin anlamını kesin olarak bilmeden yorum yapmak zorunda kalan Apollonius yorumcuları için bir mıknatıs görevi görmüştür. Yakın zamana kadar Heath’in görüşü geçerliydi: çizgiler kesitlerin normalleri olarak ele alınmalıdır. Bu durumda normal, bazen ayak olarak adlandırılan bir teğet noktasındaki bir eğriye diktir. Bir kesit Apollonius’un koordinat sistemine göre çizilirse (bkz. aşağıda Apollonius’un Yöntemleri), çap (Heath tarafından eksen olarak çevrilmiştir) x ekseninde ve tepe noktası orijinde solda olacak şekilde, önermelerin ifade biçimi minimum/maksimumların kesit ile eksen arasında bulunacağını gösterir. Heath, kesit üzerinde hem teğet noktası hem de doğrunun bir ucu olarak hizmet eden sabit bir p noktasını göz önünde bulundurarak görüşüne yönlendirilir. Bu durumda p ile eksen üzerindeki bir g noktası arasındaki minimum mesafe p’den gelen normal olmalıdır.

Modern matematikte, eğrilerin normalleri, eğrinin ayak etrafında bulunan küçük kısmının eğrilik merkezinin konumu olarak bilinir. Ayaktan merkeze olan mesafe eğrilik yarıçapıdır. İkincisi bir dairenin yarıçapıdır, ancak dairesel eğriler dışındaki eğriler için küçük yay dairesel bir yay ile yaklaştırılabilir. Dairesel olmayan eğrilerin eğriliği, örneğin konik kesitler, kesit boyunca değişmelidir. Eğrilik merkezinin bir haritası; yani, ayak kesit üzerinde hareket ettikçe bulunduğu yer, kesitin evolütü olarak adlandırılır. Böyle bir şekil, bir çizginin ardışık konumlarının kenarı, bugün zarf olarak adlandırılır.

Kitap V Önsöz

” Apollonius’tan Attalus’a, selamlar.
” Bu beşinci kitapta maksimum ve minimum doğrularla ilgili önermeleri ortaya koydum. Bilmelisiniz ki, bizden öncekiler ve çağdaşlarımız en kısa doğruların araştırılmasına sadece yüzeysel olarak değinmişler ve sadece hangi doğruların kesitlere değdiğini ve tersine hangi özellikleri nedeniyle teğet olduklarını kanıtlamışlardır. Kendi adıma, bu özellikleri ilk kitapta (ancak kanıtlarda en kısa doğrular doktrinini hiç kullanmadan), konunun üç konik kesitin üretimini ele aldığım kısmıyla yakın bir bağlantıya yerleştirmek istediğim kadarıyla kanıtladım, aynı zamanda üç kesitin her birinde, orijinal (enine) çapa atıfta bulundukları gibi sayısız özellik ve gerekli sonuçların ortaya çıktığını göstermek için. En kısa çizgileri tartıştığım önermeleri sınıflara ayırdım ve her bir durumu dikkatli bir şekilde göstererek ele aldım; ayrıca bunların araştırılmasını yukarıda bahsedilen en büyük çizgilerin araştırılmasıyla birleştirdim, çünkü bu bilimi geliştirenlerin, konunun kendi iyiliği için çalışmaya değer görünenlerden biri olmasına bakılmaksızın, problemlerin analizi ve belirlenmesi ve sentezleri hakkında bilgi edinmek için bunlara ihtiyaç duyduklarını düşündüm. Elveda.”

Kitap VI

Yalnızca Arapçadan yapılan çeviriler sayesinde bilinen VI. kitap 33 önerme içerir ki bu da herhangi bir kitap içinde en az olanıdır. Ayrıca önceki metinlerdeki hasar veya bozulma nedeniyle metinde büyük boşluklar veya eksiklikler vardır.

Konu nispeten açık ve tartışmasızdır. Önsöz 1’de “konilerin eşit ve benzer kesitleri” olduğu belirtilmektedir. Apollonius, Öklid tarafından üçgenler, dörtgenler gibi daha temel şekiller için sunulan uygunluk ve benzerlik kavramlarını konik kesitlere genişletir. Önsöz 6, “eşit ve eşit olmayan” ve “benzer ve benzemeyen” “kesit ve parçalardan” bahseder ve bazı yapısal bilgiler ekler.

Kitap VI, kitabın başındaki temel tanımlara geri dönüşü içermektedir. “Eşitlik” bir alan uygulaması ile belirlenir. Eğer bir şekil, yani bir kesit ya da parça, diğerine “uygulanırsa” (Halley’in si applicari possit altera super alteram’ı), eğer çakışıyorlarsa ve birinin hiçbir çizgisi diğerinin hiçbir çizgisini kesmiyorsa “eşittirler” (Halley’in aequales’i).

Kitap VI Önsöz

” Apollonius’tan Attalus’a, selamlar.
” Benden öncekilerin atladığı bazı diğer konuların yanı sıra, konik kesitler ve konilerin eşit ve eşit olmayan, benzer ve benzemeyen bölümleri hakkındaki önermeleri kapsayan konilerin altıncı kitabını size gönderiyorum. Özellikle, bu kitapta, verilen bir dik konide, bir kesitin verilen bir kesite eşit olarak nasıl kesileceğini ve bir dik koninin verilen bir koniye benzer olarak ve verilen bir konik kesiti içerecek şekilde nasıl tanımlanacağını bulacaksınız. Ve gerçekte bu konuları, bizden önce bu konularda yazanlardan biraz daha eksiksiz ve açık bir şekilde ele aldım. Elveda.”

Kitap VII

Yine Arapça’dan çeviri olan VII. Kitap 51 önerme içerir. Bunlar Heath’in 1896 baskısında ele aldığı son önermelerdir. Önsöz I’de Apollonius bunlardan bahsetmez, bu da ilk taslağın yazıldığı sırada bunların tanımlanacak kadar tutarlı bir biçimde var olmamış olabileceğini ima eder. Apollonius, Halley’in “de theorematis ad determinationem pertinentibus” ve Heath’in “sınırların belirlenmesini içeren teoremler” olarak çevirdiği “peri dioristikon theorematon” gibi muğlak bir dil kullanır. Bu bir tanımlama dilidir, ancak herhangi bir tanımlama yapılmamıştır. Referansın belirli bir tanım türüne olup olmadığı düşünülebilir ancak bugüne kadar inandırıcı bir şey önerilmemiştir. Apollonius’un hayatının ve kariyerinin sonlarına doğru tamamladığı VII. kitabın konusu Önsöz VII’de çaplar ve “bunlar üzerine tanımlanan şekiller” olarak belirtilmiştir ki Apollonius bunlara yoğun bir şekilde bel bağladığı için eşlenik çapları da içeriyor olmalıdır. “Sınırlar” ya da “belirlemeler” teriminin ne şekilde uygulanabileceği belirtilmemiştir.

Kitap VII Önsöz

” Apollonius’tan Attalus’a, selamlar.
” Bu mektupla birlikte size konik kesitler üzerine yedinci kitabı gönderiyorum. Bu kitapta, kesitlerin çapları ve üzerlerinde tanımlanan şekillerle ilgili çok sayıda yeni önerme yer almaktadır; ve tüm bunlar birçok problem türünde ve özellikle de olasılık koşullarının belirlenmesinde kullanılmaktadır. Bunların birkaç örneği, sekizinci kitapta tarafımdan çözülen ve gösterilen belirli konik problemlerde ortaya çıkmaktadır; bu problemler, mümkün olan en kısa sürede size göndermeye özen göstereceğim bir ek vasıtasıyla sunulacaktır. Elveda.”