Kaos Teorisi ve Yönetim

Bir kavramı, olguyu ve durumu daha iyi anlamak adına dilde ona verilen adın etimolojik kökenine bakmak her zaman iyi bir yol olagelmiştir. Kaos kelimesiYunanca kökenli olup bir şeyi doğurmak amacıyla esneyip yarılmak, bu doğrultuda açılmak anlamına gelen “khasko” fiilinden türemiştir. Kaos ise bu minvalde oluşan boşluk ve açıklık durumlarını betimlemektedir. Kelime birincil anlamıyla günümüzde evrenin düzenden önceki “karmaşık, şekilsiz, ayrışmamış, anlaşılmayan ve kontrol edilemeyen hâli olarak” anlaşılmaktadır (Altunoğlu, 2009) ki bu da aslında günümüzde evrenin oluşumundaki ilk evre için bilimsel açıdan yapılan izahata oldukça uygundur. Bu noktada kimin kimi etkilediği üzerinde düşünülmesi gereken bir konudur.

Kaos (Eski Yunanca: χάος, khaos), öte yandan dinsel açıdan ya da mitolojik açıdan bakıldığında da anlam kazanmakta ve Yunan yaratılış mitlerinde evrenin ya da kozmosun yaratılmasından önceki boşluğu ya da cennetin ve yerin ayrımının yarattığı ilk “boşluk” halini karşılamaktadır. Yunan yaratılış miti homojen bir boşluk durumu olan kaos ile başlar (Kaçmaz, 2005). Kaos yine aynı zamanda kendisinden sonra gelecek ve var olma koşulunu sağlayacak diğer tüm şeylerin ilk hali, kaynağı olarak da nitelendirilmektedir. Kaos sözcüğü günlük dilde düzensizlik, karmaşa anlamında kullanılsa da teoriye konu olduğu hali bakımından daha farklı bir anlama gelmekte ve  “düzensizliğin  içindeki  düzen”  anlamında  kullanılmaktadır  (Kendirli, 2006).

Ortaçağ dünyasına gelindiğinde ki herhangi bir konuyu Batılı kaynaklardan okuyorsak bu “a priori” dünya çoğunlukla Avrupa kıtasından ibarettir, kaos kavramı Hıristiyanların dini kitabında da geçmektedir. Bahse konu olan dönemde Avrupa’da toplumun örgütlenme şekli yayılan Hıristiyanlık dinini bir iktidar aracı olarak kullanan Katolik kilisesi tarafından oluşturulmuş, halk soylular ve kilise arasındaki bölüşümün bir objesi olarak kalmıştır. Sonrasında, Kilise’nin hakimiyet alanını doğuya genişletmek istemesi ve kurulan Haçlı orduları ile sadece İslam toplumları üzerinde değil farklı mezhebe ve inanışlara sahip ancak kendini Hıristiyan olarak tanımlayan tüm doğu toplumları üzerinde bir belirsizlik hali yani kaos oluşturmuştur. O dönemde de dünyanın en önemli şehirlerinden biri olan İstanbul’un başkent olduğu Doğu Roma İmparatorluğu da Haçlı seferleri sonucunda kurulan Latin İmparatorluğu ile kısa süreli işlevsiz kalmış ve XV. yüzyılda Fatih tarafından tamamen ortaya kaldırılışına giden yola girmiştir. Doğu Roma’nın yıkılışının getirdiği karmaşa ve belirsizlik hali beraberinde bir kaosun doğuşuna sebep olmuş ve kelimenin ilk başta tartışılan anlamına uygun bir şekilde yine kaosun içinde bir düzen oluşmuş ve bu kaos süreci sonucunda o günün Avrupa’sını ve tarihsel süreçte günümüz dünyasını şekillendiren Rönesans ve Reform hareketleri ortaya çıkmıştır (Çavuş ve diğerleri, 2016).

Kaos kavramını tanımlamak adına modern zamana yakın ifadelere bakıldığında kaos kavramının bir özelliği üzerinde durulduğu ancak kaosun bütüncül olarak almadığı sonucuna varabiliriz. Örneğin Jim Yorke‟a göre kaos, “başlangıç durumuna hassas bağlılığı bulunan bir zamansal evrimdir” ve Yorke bu tanımda kaosun etkilerinin hissedilmesi için zaman kavramına ve daha sonra ayrıntıları ile ele alınacak olan başlangıç koşullarına bağımlılık ilkesine atıfta bulunmaktadır. Ruelle ise kaosu, büyük sonuçları olabilen küçük nedenler olarak tanımlarken yine başlangıç koşullarına önem atfetmektedir. Yapılan bu tanımlar belki de kaos konusundaki ortak yanılgı olan her zaman düzenin oluşacağı varsayımına dayanmaktadır. Peki sonunda düzen oluşmayacaksa herhangi bir şartlar kümesi kaotik olarak nitelendirilebilir mi?

Kaotik sistemin bazı özelliklere sahip olması gerekmektedir. Bir yapının ya da bir düzenin eninde sonunda kaosa dönüşeceğini bilsek de gerçekte zamansal çizginin hangi noktasında kaos durumuna geçeceğini biliyor ya da tahminliyor olmak prensip olarak olanaksızdır. Bu tür yapılar, başlangıç koşullarına bağımlıdır ve lineer değillerdir. Ortaya çıkan yeni yapı, sürecin başlangıç koşullarından etkilenir ve bu koşullar belirlenemez.  Dolayısıyla, gerçekte var olan bir sistemde bulunan ancak gözlenemeyen ya da bir diğer tabirle belirlenemeyen ve klasik bilimde, hata adı verilerek tek bir kavramsal bütünlük gösteriyormuşçasına değerlendirilen kavramlar kümesinin kaosta özel bir yeri vardır. Buradan çıkaracağımız sonuç ise kaosun klasik olarak adlandırdığımız bilimden farklı şekilde değerlendirileceği ve klasik bilimin yöntem ve kabullerini yıkacağı olacaktır (Mutlu, 2006). Newton, bilimin farklı alanlarında verdiği eserler ve üzerinde çalıştığı konuların diğer çalışma alanlarından ihtiyaç duyduğu bilgilerin de peşinde emek sarf etmesi ile ve belki de tüm dünyanın onu tanımasına sebep olan ağaçtan düşen elma hikayesi sonucu ortaya koyduğu ve kütle çekimin özel bir durum olan Yerçekimi Kanunu ile tanınmaktadır. Kaos yaklaşımı, Newton’un mekanik evren görüşünü, her şeyin önceden belirlenmiş  ve  tahmin  edilebilir  olduğu  görüşünü  reddetmektedir.  Kaos  Yaklaşımı’na  göre, varlıkların ve yasaların basit, tahmin edilebilir bir kümesi olması önceden kestirilebilirlik açısından yeterli değildir, bunu matematiksel bir fonksiyon olarak düşünmek yanlış olacaktır dolayısıyla kontrol edilemeyen faktörlerin de etkisiyle karmaşık ve kestirilemeyen bir sonuca  sahip  olabilir.  Bunun  örneklerini  hava  durumu tahminlerinde, dünyanın herhangi bir yerindeki emtia borsası fiyatlarındaki değişimlerde ve  damlayan  bir  muslukta bir sonraki damlanın ne zaman düşeceğindeki belirsizlikte görebilmekteyiz (Koçel, 2003).

Günümüzde kaos kavramı toplum bilimi, yöne­tim bilimi ve eğitim bilimleri gibi sosyal bilim dallarının da çalıştığı kavramları açıklamakta kullandığı araçlar arasına girmiştir. Kaosun sosyal konularda çalışan bilimlerde kendisine yer bulmasının bazı açılım ve faydalar getirdiği açıktır. Sosyal bi­limlerin görüş ufkunu ve açıklama getireceği alanları genişletmesi ve çoklu bilim olarak tabir edilen disiplinler arası yakınlaşmayı simgeleyen yeni bir paradigmanın otaya çıkarılması konusunda avantaj sağlayan bir durum olarak değerlendirile­bilir (Akmansoy ve Kartal, 2014).

Kaos, klasik bilimin yüzyıllardır süregelen ezberinin bozulduğu nokta olarak da nitelendirilebilir ve doğrulukları üzerinde uzlaşılmış ve kesinlik arz eden bazı bilimsel gerçekler dışında, aslında kainatın içinde birçok durumun lineer olarak, sebep-sonuç ilişkisi içinde açıklanamayacağını, determinist kabullenmelerin bu konuda yetersiz kaldığını göstermektedir. Kaotik evren modelini kabul ettiğimizde denilebilir ki evrende, yerçekimi ya da aerodinamik gibi tekrarlardan oluşan ve her gözlemlendiğinde aynı sonuçları veren olgular dışında oluşan nerdeyse tüm görüngüler bu basitlikte ve kesinlikte doğrusal biçimde ve nedensellik ilkesine dayanarak açıklanamamaktadır (Dereli, Durmuşoğlu ve Kanat, 2006).

Süresiz bir kararsızlık durumu olarak da ifade edilebilecek olan kaos öte yandan öncesinde aklımıza gelmeyecek kadar fazla alanda pozitif bilimlerin de konusudur. Fizik, biyoistatistik, biyoloji, uzay bilimi, tıbbi uygulamalar ve aslında modelleme yapılan tüm çalışma alanlarında kaos bir çalışma prensibi olarak karşımıza çıkmaktadır. Deniz altında yasayan kabuklu hayvanların kabuklarının alacağı şekiller ve renk düzenlerinin hesaplanması, olası canlı yapılarının öngörüsünün bulunmasında, uzay araçlarında kullanılan mekanik sistemlerdeki basınç değişimlerinin hesaplanmasında, canlılara ait yaşamsal sistemlerinin incelenmesinde, iklim modellemelerinde, biyolojik araştırmalarda, yıldız ve galaksilerin dağılımının belirlenmesinde ve benzeri alanda uygulaması olan gözlemlenebilecek bir bilgidir.

Bu yeni bilimsel anlayış kısa sürede kendi jargonunu da üretmeye başlamış ve kainata farklı bir gözle baktığımızda gördüğümüz ancak ilk andan beri karşımızda duran bu yapılara fraktaller ve bifurkasyonlar (dallanmalar), intermitensiler ve periyodiklikler, katlanmış peçete difeomorfizmleri ve erişte haritaları gibi kendine özgü isimler vermeye başlamıştır. Bazı fizikçiler kaosu bir durumun değil bir surecin bilimin süreci olarak ve aynı zamanda bağlantılı ve benzer şekilde bir varoluşun bilimi değil bir oluşumun bilimi olarak tanımlamışlardır (Hun, 2009). Burada şüphesiz dikkat çekilen konu durağan değil devinen bir yapının var olduğudur.

Bir kar tanesinin oluşumu ki bildiğimiz kadarıyla her bir kar tanesi eşsizdir ve bir diğeri ile hiç bir zaman aynı değildir, denizdeki dalgaların oluşumu, herhangi bir kaynaktan çıkan dumanın salınımı, sıvıların akış güzergahlarının belirlenemez olması kaotik yapılanmaya örnek gösterilebilir. Bununla birlikte kaos sadece doğada gözlenen bir olgu değil sıklıkla doğanın bir parçası olarak varsayılmayan insan vücudunda da etkin olan bir dinamiktir. Buna en iyi örnek olarak insan kalbi gösterilebilir. İnsan kalbinin atışı kesinlikle kaotik bir sitemin nasıl çalıştığına örnektir. Kalbin atış hızı bazı durumlarda kalbin beklenildiği gibi çalışmaması nedeniyle belirsizlik gösterir ve kalp atışları arasında birini takip eden uzun ve kısa boşluklar ortaya çıkar, ritmik düzenden uzaklaşır. Kalbin herhangi bir atışının zamanlamasında meydana gelen çok küçük bir değişiklik, daha sonraki kalp atışlarında büyük bir değişikliğe neden olacaktır. Bu örnek, düzenli bir davranışın başlangıç koşulları değiştiğinde nasıl kaosa dönüştüğüne ilginç bir örnektir (Koçak, 2000).

Von Bertalanffy tarafından önerilen Sistem Yaklaşımı’na göre sistemler yaşamlarını sürdürmek için çevreleri ile ilişki içindedir. Bu ilişki doğal sistemler açısından enerji alışverişi anlamına gelse de sosyal sistemler açısından bu bir çok farklı yaşamsal kaynağın değiş tokuşu anlamına gelmektedir. Örneğin canlılarda olduğunu kabul edilen ve hatta canlılığın baslıca belirtisi saydığımız yasamın kendisi de bir sistemdir. İki canlının birbirleri arasında enerji alışverişinden çok daha fazlası olduğu ve bunun da aslında toplumsal yaşamın oluşmasında kilit faktör olduğu yadsınamaz bir gerçektir. Bununla birlikte organizasyonlar da birer sistemdir ve aslında temelde üretim faktörlerinin değiş tokuşu üzerine kurulu ekonomi de bu açıdan bakıldığında sistem için oldukça güzel bir örnektir. Açık ekonomilerin sistem yaklaşımını özümsemiş toplumlarda daha başarılı olduğu görülmekte, doğaya aykırı biçimde kapalı ekonomik sistemlerin de toplumları nasıl bir felakete sürüklediği görülmektedir. Cramer’e (1998) göre yaşam; enerji ile ilişkisi bakımından, karmaşa (kaos) ile düzen arasında gelip giden bir değerler dizisidir. Ölümün aslında bozulamayacak bir düzen anlamına da gelmesi ve kararlılık hali kaosun yaşam açısından önemini belirtmektedir. Canlılar için ölüm bir anlamda çevre ile ilişkinin geri döndürülemez biçimde ve süresiz olarak kopması demektir (Erdoğan, 2012).

Sistemler arası ilişkilerdeki tüm değişkenler önceden tüm ayrıntılarıyla belirlenebilecek ilişkiler otaya koymazlar. Kaotik durumlar, öngörülebilirlik ve periyodiklik ile çelişen, kesin olmama durumunu göstermektedir. Isaac Newton’ın hareket yasaları ve evrensel çekim yasasında belirtilen teori, dünyadaki ve diğer gezegenlerdeki hareketlerin düzenliliği hakkındadır ve buna göre dünyanın da içinde bulunduğu sistemin merkez noktasındaki yıldız olan güneşin ve onun çekim kuvveti ile bükülen uzay-zamanda gezegenlerin konum ve hareketleri, geçmiş ve gelecek zamanlardaki konum ve hareketleri belirlidir Doğa bilimlerindeki klasik yöntem, Newton’un da varsaydığı determinizm yasaları gibi kesinlik arz eder gibi görünse de bunun sebebi değişkenlerin azlığı ve görece olarak bazılarının devamlı ve yeterli etkiye sahip olamamasından kaynaklanmaktadır ancak evrensel boyuta çıktığımızda bu kaotik yapı daha görünür hale gelmektedir (Koçak, 2000).

Kaos kavramının bilimin radarına girmesi ve Kaos Teorisi olarak adlandırılabilecek olan evrenin işleyişine dair açıklamanın ortaya atılması XIX. yüzyılın sonlarında Fransız matematikçi Jules Henri Poincaré’nin çalışmaları ile başlamıştır. Dinamik sistemlerin çalışma prensipleri üzerinde çalışmış olan tüm klasik fizikçi ve matematikçiler arasında kaos kavramını en iyi anlayan bilim adamı Poincaré olmuştur. Poincaré “Bilim ve Yöntemler” adını verdiği eserinde, çok değişkenli sistemlerin kalıcı çözümlerinin olmadığını, çözümlerinin sonsuz bir şekilde sürebilen oynak bir durum alacağını ve bunun da sistemlerde geleceğin tahminini imkansız kılacağını ifade etmektedir. Poincaré ‘ye göre dikkatlerimizden kaçan küçücük noktalardan biri ya da başka bir deyişle sistemin işleyişinde etkili olan ancak göz ardı edilen faktörlerden biri sonuçlar üzerinde öylesine büyük ve önemli sonuçlara neden olur ki gözlemci bu sonucun rastlantı sonucu ortaya çıktığını savlayabilir.Doğanın işleyiş mekanizmasını ve evrenin başlangıç anındaki durumunu eksiksiz bir şekilde bilseydik ki fizikte uzun süredir çalışılan en önemli konulardan biridir, evrenin o ilk anını izleyen daha sonraki anlardan herhangi birinde hangi durumda olacağını da tam olarak modellememiz mümkün olabilirdi. Doğanın mekanizması hakkında bilgimizin bu denli bir tamlık gösterdiği durumda bile yaklaşık da olsa bilgiye sahip olduğumuz söylenebilir ve ancak bu şartlar halinde olan ve olması gerektiğini düşündüğümüz durumların uyumlu ya da uyumsuz olduğu öne sürülebilir. Ancak başlangıç şartlarında küçük farklar, ölçüm yanlışları, göz ardı edilen değişiklikler tahmin edilemez farklar doğuracaktır. Bu durumda öngörüde bulunmak olanaksız bir ha almaktadır. (Öge, 2005).

Kaos teorisini anlamak ve anlatmak için matematiğin  ne kadar önemli olduğunu ifade eden ve kendisi de bir matematikçi olan Poincaré’nin geliştirdiği yaklaşım günümüzde başlangıç ​​koşullarına son derece hassas olan dinamik sistemlerin davranışına odaklanan bir matematik dalıdır. Bir  olayın  sonucunu  bilebilmek,  onun  başlangıç  şartları  bilgisinin  tüm ayrıntılarıyla  bilinmesini  gerektirir.  Örneğin uçurumun başından yuvarlanan bir kaya parçası daha büyük bir kitlenin de hareketini tetikler, vadideki akarsuyun yolunu tıkayan taş parçaları suyun akışını engeller ve suyun sığ hale gelmesi sonucu açığa çıkan balık orada geçmekte olan ayı tarafından fark edilir ve ona yemek olmaktan kurtulamaz, ayı ise yediği bu balıktaki bir bakteri yüzünden enfeksiyon kapar ve uzun ve acı dolu bir ölüm sürecine girer. Bu durum balığın mı yoksa ayının mı yoksa hiçbirinin mi öngörebileceği bir durumdu? Öte yandan o ilk taşın düşmesinde etkili olan faktörlerden biri taşın anakayayla bağlantısını gece-gündüz sıcaklık farklarından dolayı çözen bir yağmur damlası olabilir miydi? O halde bir yağmur damlası bir ayıyı öldürdü diyebilir miyiz? Böyle  bir  bilgiyi  elde  etmek  ise  imkansız  olduğundan, olayların sonuçları sistemli biçimde bilinebilirliğe sahip değildir ancak, olasılıklara dayalı olarak tahmin edilebilirler. Bu durum her ne kadar fazlasıyla zorlama bir senaryo gibi görünse de evrenimiz aşağı yukarı tam da bu şekilde işlemektedir.

Her ne kadar kaos kavramını ilk ortaya süren kişi olarak Poincaré kabul edilse de teoriye en önemli katkı 1960 yılında MIT’ de meteoroloji profesörü olan Lorenz tarafından yapılmıştır. Lorenz, hava tahmin raporu hazırlayabilmek için bilgisayarına girdiği veriler üzerinde çok küçük değişiklikler yapmış ve sonuçta bulduğu sıcaklık değerlerini grafik üzerinde göstermiştir. Bu küçük farklılıklara sahip değişkenler üzerindeki çok küçük değişikliklerin fonksiyonlara ait grafiklerde anlamlı bir farklılığa yol açmayacağını beklerken sonuçta ortaya birbirinden oldukça farklı sonuçlar çıkmıştır. Lorenz’in elde ettiği ve Şekil 1’de gösterilen bu grafikte, koordinat sisteminin yatay düzlemi günleri, düşey düzlemi ise sıcaklık değerlerini göstermekte idi. Bu grafiğin eğrileri, beklenen iniş ve çıkışları sergiliyordu. Grafik uzun dönemde bir düzene oturmuş gibi görünmekteydi ve söz konusu grafik bir kelebeğe benzer desen oluşturmakta idi. Lorenz’in bu durum karşısındaki yorumu uzun vadede doğru ve güvenilir bir hava tahmininin modelin sergilemiş olduğu kaotik davranış nedeniyle belli bir süreyi aşamayacağı, bu nedenle periyodik olmayan davranış özellikleri gösteren hiçbir sistemde öngörü yapmanın mümkün olmadığı şeklinde idi.

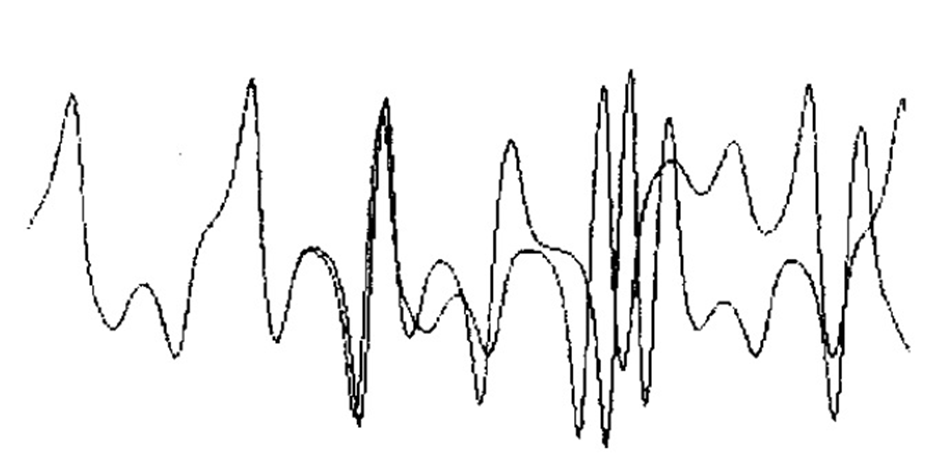
Şekil 1: Lorenz’in Hava Tahmini Grafiği

Kaos  teorisine  yaptığı ampirik çalışma ile önemli  katkı sunan  Edward  Lorenz  çalışmasının  sonunda  kelebeğin  kanatlarına  benzetilen,  Lorenz  Çekicisi  olarak  bilinen  şekle  yer  vermiştir.  Düzensiz  bir  veri  akışı  içinde  düzenli bir sonuç değerleri gösteren yapının  bulunduğunun  görsel ifadesi olarak  kabul edilen bu şekil ile ortaya çıkan her olayın ne kadar  karmaşık  görünse  de  kendi  içinde  bir  düzeninin  olduğu görülmektedir. Lorenz çekicisi (Lorenz sistemi olarak da bilinir) bir , Lorenz denklemleri adı verilen adi diferansiyel denklem sistemidir. Belirli parametre değerleri ve başlangıç ​​koşullarındaki küçük değişiklikler için kaotik çözümlere sahip olmaları karakteristik özellikleridir. Özellikle, Lorenz çekicisi, Lorenz sistemine ait sonuç değerlerdi çizildiği zaman bir kelebeğe ya da sekiz rakamına, ya da sonsuz işaretine benzeyen kaotik bir çözüm kümesidir.

Lorenz, kaotik sistemlerin iki temel özelliğini üzerinden ileri sürdüğü teoriyi açıklamaya çalışmıştır. Bunlardan ilki başlangıç durumuna hassas bağımlılıktır. Farklı kaynaklarda farklı yerlerin adı zikredilmesine rağmen genellikle Brezilya’da kanatlarını çarpan bir kelebeğin ABD’de tetiklediği olaylar dizisi sonucu kasırgaya neden olması olarak örneklenen bu durum, kelebeğin yarattığı etki üzerinden kelebek etkisi olarak isimlendirilmiş ve popüler kültürde de kendine oldukça fazla yer bulmuştur. Kelebek etkisi, karmaşık sistemlerde çok küçük, önemsiz gibi görünen ve dikkate  alınmayan  bir  etki  beklenmeyen  büyük  sonuçlar  yaratabilme durumu olarak ifade edilebilir. Rastgele olmama durumuise evrendeki bir çok işleyişin aslında kaotik bir yapıya, tüm kaotik yapıların  ise  kendi  içerisinde  bir  düzene  sahip  olduğu  anlamına  gelmektedir.  Yani  düzensizliğin  kendi  içinde  bir  düzeni  vardır. Latince ifadesi ile “Ordo ab Chao” yani kaostan doğan düzen klasik bilim paradigmasının determinist anlayışına  uymamakta ve  dinamik bir süreç özelliği göstermektedir.

Lorenz bu saptamasını her ne kadar bilimsel bir makale olarak yayınlasa da bu makale sadece meteorologlar için yayınlanan bir dergide toplumun ilgisini çekmekten uzak bir şekilde kalmıştır. Bununla birlikte eş zamanlı olarak Yoshisuke Ueda adında bir bilim insanı kaotik fenomeni analog bir bilgisayar kullanarak tespit etmiştir. Ancak akademik danışmanı Profesör Hayashi, kaotik bir işleyişe inanmadığı için Ueda’ya bulgularını yayınlama izni vermedi. Ueda bu yayını buluş tarihinden oldukça sonra yayınlayabilmiştir ve bu tarihten sonra kaos, bilim insanlarının dikkatlerini oldukça çeken bir konu olmuştur (Uçar, 2010).

Kaos Teorisi’ne göre; düzen belirli bir zaman sonra düzensizliği oluşturabilir ve bunun tersi olarak düzensizlik durumunun içinde düzen de saklıdır ve yeteri kadar denemeden sonra düzen hali tekrar kurulacaktır. Aslında düzen denilen durum düzensizlik halinin özel bir durumudur ve onu gözlemleyen kişiye de bağlıdır denilebilir. Bunun yanı sıra oluşan bu yeni düzen halinde bir uzlaşma ve bağlılıktan bahsetmek mümkündür ve bu yeni düzen kestirilemez ve çoğu zaman tersinemez bir yöne doğru gelişim gösterir.

Rockler’a  göre Kaos Teorisi evrendeki lineer olmayan modelleri açıklamamızda bize yardımcı olur ve Newton’ın mekanik modeli ile atom altı parçacıkları inceleme konusu edinen kuantum fiziğinin  rastgeleliği arasında bir bağ oluşturmaktadır. Kaos, küçük farklılıkların kestirilemez büyük sonuçlar doğurduğunu gösterir ve insana dair sistemler de  en iyi biçimde kaosu anlama yoluyla açıklanabilir. Bu anlayış bize aynı zamanda evrenin de açık bir sistem olduğu bilgisini iletmektedir (Altun, 2001).

Determinizm ve Kaos

Determinizm veya belirlenircilik evrenin işleyişinin bilimsel yasalarla belirlenmiş olduğunu ve bu belirlenmiş olayların gerçekleşmelerinin bir rastgelelik değil zorunluluk sonucu olduğunu öne süren öğretidir. Buna göre her şey önceden daha önceki olanların bir sonucu olarak belirlenmiştir ve değişmesi mümkün değildir. Bu görüş başta etik olmak üzere felsefenin çeşitli dallarının uğraş ve çalışma alanına dair bir görüştür. İslamiyet de dahil olmak üzere çeşitli dinsel öğretilerde de var olan kadercilik anlayışı da bu öğretinin bir tezahürüdür ve teolojik determinizm adı verilmektedir. Bilim tarihinde Pierre-Simon de Laplace tarafından yayınlanan Laplace’ın Şeytanı veya Cini adlı eserde bilimsel determinizmin ilk örneği bulunmaktadır. Buna göre eğer herhangi biri evrendeki tüm atomların yerini ve momentumunu tam kesinlikle biliyor olsa ve tüm etkileri hesaplayabilecek bir bilgiye sahip olsa geçmiş ve gelecekteki her şeyin herhangi bir anda nasıl olacağını hesaplayabilir durumda olacaktır. Laplace’ın bu savına karşı çıkan görüşler arasında termodinamik tersinemezcilik, kuantum mekaniği tersinemezciliği ve Kantor diyagonalizasyonu sayılabilir. Bunlarla birlikte Kaos Teorisi de bu sava doğası gereği karşı çıkmaktadır. Nedensellik prensibi determinizm anlayışında temel prensip olarak kabul edilmektedir. Çünkü determinizme göre evrende akla uygun bir yapı ve düzen vardır, dolayısıyla belirli nedenlerin veya durumların bilgisine sahip olunduğunda, o nedenlerin veya durumların ortaya çıkartacağı olayların bilgisini elde etmek mümkündür (Alpar, 2012). Ancak bu yaklaşımın günümüzde karşılığının olduğunu söylemek oldukça güçtür.

Kaos teorisinin, olguların birçok farklı de­ğişkenden etkilendiği ve olayların nedenlerinin kaotik (çok değişkenli ve karmaşık) olduğu yaklaşımı, klasik bilim paradigmasının determinizm olarak ifade edilen “lineer nedensellik” kuralı ile uyuşmamaktadır. Klasik bilim yöntemi, olgular arasındaki neden-sonuç ilişki­lerini doğrusal ve tek yönlü bir şekilde ele almaktadır. Yani X, Y’nin nedeniyse; Y, X’in nedeni olmamalıdır. Daha geniş ifade etmek gerekir­se; evrendeki her şey neden-sonuç ilişkisiyle birbirine bağlıdır. Doğayla ilgili bu ontolojik-deterministik anla­yış şu şekilde formüle edilebilir: A, B’nin nedeni; B, C’nin nedeni; C, X’in nedeni; X, Y’nin nedeni; Y ise Z’nin nedenidir (Biçici, 2016).

Determinizm anlayışının en önemli sonuçlarından biri de özgür irade kavramına karşı olmasıdır. Buna göre aldığımız kararlar, düşüncelerimiz, eylemlerimiz , ahlaki tercihlerimiz belirlenmiş ve kesin kurallar içerisindedir ve özgür irade bir yanılsamadan ibarettir. Özgür irade ile verilen kararlar sonucu oluşan ve kişiye özgü sanılan hareketlerimiz sadece bilimsel yasaların bu işleyişinden ibarettir ve  insan iradesi denilen olgu nedenler zinciri ile gelişen bir durumdur ve bu durumda bireyin içsel bir etkisi bulunmamaktadır. Nedensellik ilkesi determinizmin temel taşıdır. Evrende bir düzen bulunmaktadır ve nedenler-sonuçlar bu düzen içerisinde işler. Bu düzenin işleyiş mekanizması çözüldüğünde nedenler ve sonuçlar açıklanıp daha sonra gelişecek olayların bilgisini elde etmek mümkün olacaktır. Spinoza’nın determinizm anlayışına göre ise aklın tamamen objektif oluşu mutlak determinizm olarak nitelendirilir. Aklın tamamen objektif oluşu düşüncesi oldukça iddialı bir düşünce gibi dursa da pozitivist-aydınlanmacı dönemde çok da karşı çıkılan bir düşünce yapısının ürünü değildir. Kaos teorisinin, olguların birçok farklı değişkenden etkilendiği ve olayların nedenlerinin kaotik (çok  değişkenli  ve  karmaşık)  olduğu  yaklaşımı,  klasik  bilim paradigmasının determinizm olarak ifade edilen “lineer nedensellik” kuralı ile uyuşmamaktadır. Sistem önceki durumun belirli kurallar altında değiştiğini varsayan determinizmin ne kadar mekanik ve dışa kapalı bir model olduğunu anlamak oldukça önemlidir. Bu görüş Antik Yunan’a kadar uzanmaktadır. Modern bilime ise bu önceden belirlenmiş olan işleyiş mekanizmasını yani sebep-sonuç ilişkilerini araştırmak amacıyla girmiş ve modern bilimin temelini oluşturmuştur. Bilimsel deterministik modele göre evren, herhangi bir rastgelelik göstermeden mükemmel bir makine gibi çalışır. Bu düşünce Isaac Newton ile modern bilimin temel referans noktası haline gelmiştir (Tosun, 2006).

Newton çalışmalar yaptığı bir çok bilim alanının yanında matematik alanında da “Philosophiae Naturalis Principia Mathematica” (Doğa Felsefesinin Matematiksel İlkeleri) adlı önemli bir esere imza atmıştır.  Newton’ın bu eserinde ifade ettiği matematiksel prensipler ile doğa ve sistemlerin bütünüyle anlaşılabileceği savunularak, bilimsel düşüncenin temeli oluşturulmuştur. Bu düşüncede evrenin zamanı gösteren bir saat gibi, tek bir yöne doğru işlediği başka bir deyişle lineer olduğu ve durumun bir anı hakkında eksiksiz bilgiye sahip olunursa geri kalanının da bulunabileceği savunulmuştur. Daha önce bahsedildiği gibi Laplace’ e göre, evrenin bugünkü durumu, önceki durumunun sonucu, sonraki durumunun ise nedenidir. Determinizmin matematiksel dili kelimenin tam anlamıyla basittir ki başlangıç koşullarının bilinmesi, ona uyan biricik ve kesin analitik çözümü, çözüm uzayından seçilebileceğini ifade etmektedir. Bu çözüm bir fonksiyonla ifade edilirse, herhangi bir t anında sistemin durumunu biliyor isek, f fonksiyonunu biliyoruz demektir. Artık her a değeri için f(t+a) ve f(t-a) fonksiyonlarının değerlerini hesaplamak mümkündür. Matematiksel açıdan bakınca çözüm fonksiyonunun grafiği üstünde gerçekleşen bu olgu, söz konusu dinamik sistemin önceden belirlenebilen çözüm kümleri dahilinde oluşturulan kendi yörüngesi üzerinde belli bir noktadan ileri ve aynı şekilde geri hareket ettirilebilmesi demektir (Tosun, 2006). Bu tersinemezciliğin de aslında inkarı anlamına gelmektedir.

Klasik  paradigma,  doğayla  ilgili  olarak ontolojik  deterministik bir yaklaşım benimsemiş ve bunun karşılığında Kaos Teorisi doğanın belirlenemez ve kaotik bir  yapısı olduğunu ileri sürmektedir. Daha açık bir ifadeyle; dünyadaki birçok olay  daha önce de örnekleri verilmiş olan bir  kar  tanesinin  oluşumu,  gazların  salınım hareketleri,  ağaç  köklerinin  gelişimi,  kuş  sürülerinin hareketleri ve denizdeki  dalgalar aslında  kaotik  birer modele sahiptir ve doğrusallık göstermezler.Bütün bu kaotik yapılanmalar aynı zamanda gelişi güzel de değildir ve  kendi  içinde  bir  düzene  sahiptir.  Bununla  beraber  kaos, matematiksel olarak olasılık kavramı ile  de ilişkilidir. Örneğin; bilardo oyunundaki  başlangıç  vuruşu  ondan  sonra  gelecek  olan  vuruşları  etkilemekte ve yine her seferinde  her  topun  diğer  bir  topa  çarpması veya vuran bireyin motivasyon durumu gibi her bir vuruş için pek çok farklı değişken de olduğundan, her vuruş sonsuza yakınsayan bir olasılıklar kümesinden bahsetmek doğru olacaktır. Burada olasılıkların aritmetik değil logaritmik bir artış gösterdiğini anlamak önemlidir.

Kaos  teorisi  ile  klasik  fiziğin  determinist  anlayışın açıklamakta zorlandığı dinamik  sistemler açıklamaya kavuşmaktadır. Atom altı parçacıklar ile ilgilenen Kuantum Teorisi atom üstü evrendeki modelleri nasıl yerle bir ettiyse, Kaos Teorisi de determinizme ironik bir şekilde belki de geri döndürülemeyecek bir darbe vurmuştur. Determinizmin geçerli olabilmesi için sistemin analitik çözümünün ve iyi belirlenmiş başlangıç koşullarının belirlenmesi gerekmektedir. Bu durum belirlenebilir sayıda faktörün etki ettiği ve kapalı sistemlerde geçerli olsa da tekrarlanamayan ve öngörülemeyen etkiye sahip sonsuz sayıda değişkenin rol aldığı açık sistemlerde işlemesi imkansızdır (Karaçay, 2004).

Sosyal (toplum) bilimlerin varlık sebebi insanların ve insan topluluklarının davranış kalıplarını anlamak ve açıklamaktır.  Lakin her davranışı açıklayan genel-geçer ilkeler bulunmamakta ve bu durum da sosyal   bilimlerin  klasik  bilim  yaklaşımı ile  bilim  olma  konusunda eksik olduğu şeklinde yorumlanmaktadır. Zira bu anlayış bilimden sürekli tekrarlanabilir ve dolayısıyla statik açıklamalar beklemekte ancak insan faktörünün getirdiği kestirilemezlik bunu engellemektedir. İnsan davranışını etkileyen ve oluşturan birçok değişkenin olması klasik bilim anlayışı çerçevesinde pozitivist-determinist  yaklaşımının  uygun  olmadığını göstermektedir. Öte yandan   fizik biliminde yeni  teorilerinin yani evrenin işleyişine dair yeni açıklamaların ortaya  çıkmasına neden olan kuantum seviyesindeki bulgular arttıkça,  Einstein’ın  “Tanrı  zar  atmaz”  şeklindeki  ifadesiyle  anlatmaya  çalıştığı ontolojik-deterministik kavramlar sorgulanır hale gelmiştir (Wichmann, 1993). Bunun sonucunda da yeni kavramlar, ilkeler,  teoriler  ortaya  konmuştur. 

Özellikle  Heisenberg’in belirsizlik ilkesi ve üçüncü ihtimallerin göz ardı edilmemesi  gerektiği, Poincaré’nin Üç Cisim Problemi için önerdiği çözüm ve Lorenz’in  doğa  olaylarının  başlangıç  durumuna  hassas  bağımlılığı  ve  gerçekliğin kaotik yapıya sahip olması şeklinde ifade  ettiği  ilkeler yeni bir bilimsel paradigmayı dayatmaktadır. Belirsizlik ilkesi, Werner Heisenberg tarafından öne sürülmüş olan ve bir atom altı parçacığın momentumunun ve konumunun aynı anda tam doğrulukla ölçülemeyeceğini savunan ilkedir. Belirsizlik ilkesini daha da genellenmiş olarak anlatmak istersek şunları söyleyebiliriz. Kökleşik (klasik, deterministik) fizikten ayrı olarak kuantum fiziğine göre her fiziksel niceliğe denk gelen bir reel sayı değil, bir işlemci bulunmaktadır. Bu işlemciler, sayısal değerler ile değil matrisler ile temsil edilir. Dolayısıyla, kuantum mekaniğinde ölçülen fiziksel niceliğin ölçüm sırası önemlidir. Herhangi iki fiziksel niceliğe denk gelen iki işlemci yer değiştiremiyorsa bu iki niceliğin (örneğin: momentum ve konum) aynı anda ölçülmesi olanaksızdır.

Kaos Olgusuna İlişkin Kavramlar

Bu noktada Kaos Teorisi ile ilişkili kavramlardan kısaca söz etmek gerekirse; etkileşim alanı, başlangıç koşulları, çekim merkezi, çatallaşma, kritik nokta ve yineleme kavramlarını açıklamak yerinde olacaktır. Etkileşim alanı, bir sistemin içinde gerçekleşebilecek tüm olası durumların birleşimini ifade etmektedir. Yukarıdaki fonksiyon örneği üzerinden anlatmak gerekirse tüm değerler için oluşturulan çözüm kümesi eşleşmeleri o fonksiyonun etkileşim alanını oluşturacaktır. Başlangıç koşulları, bir modelin t=0 anındaki sahip olduğu parametreler olarak nitelendirilebilir. Çekim merkezi, kaotik değişim durumları içerisinde oluşan geçici kararlılık hallerini ifade etmek için kullanılmaktadır. Çatallaşma, sistemin geri döndürülemeyecek bir şekilde iki farklı sisteme bölünmesi durumunu tanımlamaktadır. Ekonomik sistemlerde ve özellikle son yıllarda önemli bir fenomen olan kripto para birimlerinin işleyiş sistemlerinden olan blok zincirlerinde meydana gelen hard-forking durumu buna güncel bir örnek teşkil etmektedir. Kritik nokta (edge of chaos) ise sistemin yeni bir davranışsal durum göstereceği niteliksel durumdur. Son olarak yineleme ise periyodik olmayan değişim döngülerinin farklı koşullar altında başlangıç noktasına geri dönmesi durumunu ifade etmektedir.

Başlangıç Durumuna Hassas Bağlılık (Kelebek Etkisi)

Kaos Teorisi’nin en temel kavramlarından biri olan ve  ‘Kelebek Etkisi’ olarak bilinen kavram ilk defa Lorenz tarafından kullanılmıştır. Lorenz’in hava tahminlerine ilişkin verilerini bilgisayara girdikten sonra elde ettiği grafiğin görüntüsü, Şekil 2’de gösterildiği gibi, bir kelebeğin kanatlarını anımsatmaktadır. Kelebek etkisi adını hem grafiğin kelebeğe benzemesinden hem de etkiyi açıklamakta kullanılan kelebek analojisinden almaktadır.

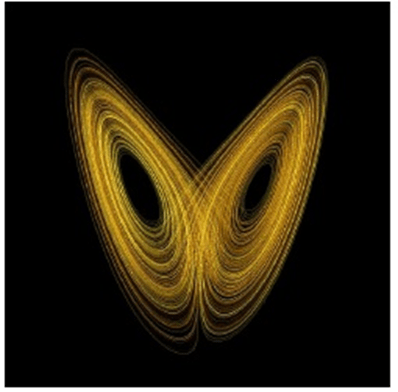
  Şekil 2: Lorenz Çekeri

Kaotik hareketin iki ana temel bileşeni başlangıç koşullarına hassas bağımlılık göstermekle birlikte sistemin yaklaşık olarak başlangıç koşullarına yönelik hareket ediyor olmasıdır. Hava durumu gibi karmaşık sistemlerin belirli bir zamanın ötesinde tahmin edilmesinin imkansız olmasını nedeni başlangıçtaki atmosferik koşulların tam olarak bilinemiyor olmasından kaynaklanmaktadır. Dinamik bir sistem eğer noktalar zaman içinde üstel bir  oranda rastgele bir şekilde örtüşmekteyse, başlangıç koşullarına hassas bağımlılık gösteriyor demektir. Bu tanım esasında topolojik bir ifade değil ölçümsel bir ifadedir. Gleick ve Berry (1987) teorinin içinde “Doğrusal (lineer) sistemlerde küçük nedenlerin etkisi küçük, büyük nedenlerin etkisi büyük olur. Ayrıca doğrusal sistemlerde bütün öğelerin toplamına eşittir yani ne fazla ne de eksiktir. Bu nedenle doğrusal bir sistem kararlıdır, öngörülebilir, kesindir ve dolayısıyla kaosa yer vermez” ifadelerini kullanmaktadır (Mermer, 2017). 

Gerçek hayatta olduğu gibi bilimde de, bir takım zincirleme olaylarla küçük değişiklikleri büyük ve önemli sorunlar haline getiren bir kriz noktasının olduğu kabul edilir. Kaos ise, işte bu noktaların her yerde oldukları manasına gelmektedir (Gleick, 1995:67) Başlangıç koşullarına hassas bağlılık kavramını açıklamak için bu durumun kaotik olan ve kaotik olmayan sistemlerde mukayeseli açıklamasını yapmak yerinde olacaktır.. Kaotik olmayan modellerde başlangıçta yapılan küçük bir değişiklik, sadece zamanla doğrusal olarak büyüyen başka bir değişikliğe yol açarken kaotik sistemlerde bu üstel bir büyümeye sebep olur. Bunun anlamı, “sistemin içindeki küçük bir değişikliğin bir süre sonra çok büyük bir değişikliğe neden olabileceğidir. (Uçar, 2010).

Griths ve arkadaşlarına (1991) göre, yönetimcilerin görüşü büyük problemleri çözmek için ihtiyaç duyulan ve belirtilerin ne olduğuna yönelik bilginin çok ender görünür olduğudur. büyük problemlerin hazır paketlerde ve çözülmeye hazır halde gelmediğini söylerler. Kelebek etkisi, bu ipuçları ile, yöneticilere zararsız görülen durumları çok büyük olaylara dönüşebileceğinin sinyalini verir (Akbaba ve Altun, 2001). Kelebek etkisi, günümüzdeki küresel ilişkilerde çok rahat izleyebileceğimiz olay ve ilişkilerin de açıklanmasında kullanılabilecek bir kavram haline gelmiştir (Fındık, 2004).

Fraktal Geometri

Matematikte bir fraktal, Hausdorff boyutunun kesinlikle topolojik boyutu aştığı bir Öklid uzayının alt kümesidir. Fraktaller, hemen hemen her boyuttaki küçültme ve büyütme sonucunda geometrik olarak aynı görülme eğilimindedirler. Bu gittikçe artan küçük ölçeklerdeki benzer desenlere kendi kendine benzerlik adı verilmektedir (Boeing, 2016) . Bu benzerlik her boyutta tam olarak aynı ise buna afine yani sonsuz benzerlik adı verilir. Fraktal geometri, matematiğin topoloji dalının çalışma konusudur. Fraktallerin sonlu geometrik şekillerden farklı olmasının nedeni ölçeklenme biçimleridir. Bir çokgenin kenar uzunluklarını iki katına çıkarmak alanını çokgenin içinde bulunduğu alanın boyutu üzerinde yani iki üzeri iki dört katına çıkarmak anlamına gelmektedir. Aynı şekilde bir kürenin yarıçapı iki katına çıkarsa hacmi kürenin içinde bulunduğu boyut kadar üstelenir yani iki üzeri üç olmak üzere sekiz katına çıkar. Ancak eğer fraktallerin uzunlukları iki katına çıkarsa fraktalin uzamsal içeriği her zaman bir tam sayı olmayan bir güç üzerinde yükseltilir. Bu güç fraktalin fraktal boyutu olarak adlandırılır ve genellikle fraktalin topolojik boyutunu aşar. Mandelbrot doğada var olan doğrusal olmayan desenleri incelemiş ve bu düzensizliği farklı ölçeklerde incelemek gerektiğini ileri sürmüştür (Diker ve Çamlıbel, 2003).

İlk olarak 1975’te Polonya asıllı matematikçi Benoit Mandelbrot tarafından ortaya çıkarılan fraktal geometri “doğanın geometrisi” olarak da bilinir. Fraktal geometri, evrende kendi kendini tekrar eden ama sonsuza kadar küçülen şekilleri inceler. Kendine benzer bir cisimde yine cismi oluşturan parçalar ya da bileşenler cismin bütününü izler. Düzensiz olarak gözüken ayrıntı ve desenler iterasyonlar (matematiksel tekrarlama) yardımıyla giderek küçülen ölçeklerde yinelenir ve soyut nesnelerde sonsuza kadar sürdürülebilir. Yahut bunun tam tersi olarak, belli bir ölçekte büyütme yapıldığında soyut boyutlarda desen ve cisim bileşenleri sonsuza yaklaşırken yine cismin bütününe benzeyecektir.  (Kılıç, 2010). Doğada bulunan fraktal desenlerine deniz yosunları, DNA, yıldırımlar, keçi boynuzları, ananaslar, Satürn’ün halkaları,  Romanesco brokolisi ve kar taneleri örnek verilebilir.

Fraktal geometrinin tasvir ettiği evren, yuvarlak ya da düz olmayan ancak aksine doğadaki kaotik yapıyı ifade eden bozuk şekillerden oluşan bir evrendir. Fraktal geometri, nesnelerin sadeleştirilmiş görünümlerini değil, gerçekten sahip oldukları biçimleri veren bir geometridir. geometri ile fizik dünyanın dingin ve basite indirgenmiş bir tasviri değil, dinamik yönünün ifadesi mümkün hale gelmiştir. Bu dönüşümü kozmostan kaosa geçiş olarak düşünmek de mümkündür (Ural, 2005).

Fraktal kelimesi Latince fraktus (kırık taş) kelimesinden türetilmiştir. Öklid geometrisinin idealize ettiği doğrusal ve tam sayı boyutlu evren ve doğa tasviri, hesaplamalarda kolaylıklar sağlayan ideal bir modeldir ancak doğanın gerçek yapısını tam olarak anlatmamaktadır. Öklid geometrisi için insanların doğayı anlama çabalarının sonucu olan bir sadeleştirme ve basitleştirme çabasının ürünü olarak değerlendirmek Öklid geometrisine de gerekli değeri vermeyi sağlayacaktır. Öte yandan evrenin büyüklüğü ve sonsuzluğunun anlaşılabilmesi ancak fraktal geometri sayesinde gerçekleşecektir (Kılıç, 2010).

Kendine benzerliğin çoğaltılması ile elde edilen fraktal boyut kavramı, yukarıdaki açıklamalardan da anlaşılabileceği gibi, en basta matematiksel düzlemde tanımlanmış bir kavramdır. Ancak bu matematiksel düzlemdeki ideal tekrarlamalar gerçeklikte alanında olası olmayıp bir alt ve üst sınır bulunmaktadır. (Erdoğan, 2012).

Kendi Kendine Örgütlenme

Kendi kendine ya da kendiliğinden örgütlenme başlangıçta düzensiz olan bir sistemin parçaları arasındaki içsel ilişkilerden kaynaklanan bir genel düzen biçimidir. Bu kendiliğinden örgütlenme süreci dışarıdan bir etkiye gerek olmadan sistem içinde yeterli enerji mevcut olduğunda oluşabilmektedir. Olumlu geri besleme ile güçlendirilmiş rastgele dalgalanmalar tarafından tetiklenir. Sonuç olarak ortaya çıkan yapı merkezilikten uzak bir özellik sergilemekte ve yapı tüm bileşenlere dağılmış durumdadır ve bu nedenle kendi kendini onarma becerisine sahiptir. Kaos Teorisi açısından kendi kendine örgütlenme durumları fırtınalı bir kaos denizinde bir sığınma sağlayan öngörülebilirlik adacıkları olarak da düşünülebilir.

Açık sistem çevresi ile devamlı etkileşim halinde olan sistemlere verilen addır. Sistemler kararlılıktan uzaklaştıklarında, kendiliğinden yeni bir yapı oluştururlar ve yeni denge noktaları bulurlar. Bu duruma kendi kendine organizasyon adı verilmektedir (Farazmand, 2003). Kendi kendini örgütleyebilen karmaşık sistemler bir seviyeden sonra yeni dengeler oluşturamazlar ise ya daha karmaşık (daha yenilikçi) ya da daha az karmaşık (durağan, sıradan) olan iki seçenekten birine yönelebilir. (Öztaş, 2015:.246). Modern bilim insanlığa çeşitli araçlar ile bir çok olgu üzerinde kontrol imkanı sağlarken doğanın tam anlamıyla kontrol alanında olmadığı gerçeğini ise unutturmaktadır. Örgütlerde de yöneticiler sistemin bileşenlerini tanımlayıp, bileşenlerin nasıl birlikte çalışacağını belirleyerek is ortamındaki işleyiş mekanizmasını kontrol etmek isterler ancak tüm etkileyen faktörlerin kontrol edilmesinin mümkün değildir ve bu yönetsel anlamda başarısızlığın sebebi olabilmektedir. Nitekim karmaşık sistemlerin birbirleri ile olan girift ilişkisi ve liderlerde görülen objektiflik sorunu nedeniyle yöneticilere tüm çevreyi kontrol etmeyi amaçlamaları yerine çevreyi anlayıp, çevrenin bir parçası olmaları önerilmektedir (Styhre, 2002). Birçok karmaşık sistem değişim ve durağanlığın dinamik dengesinde bulunmaktadır. Karmaşık sistemin kararlılığını yitirdiğinde sistemin parçaları çevreye adapte olur (Amagoh, 2008).

Rastgele olmamak

Kaos teorisinin bu ikinci ilkesi, evrende gerçekleşen her durumun kesinlikle bir parametreye bağlı olarak geliştiğini ifade etmektedir. Hava durumunu kaos teorisiyle açıklamaya çalışan Edward Lorenz, Lorenz Kelebeği olarak bilinen çalışması ile esasen hiçbir sonucun tesadüfi olmadığını ifade etmektedir. Kaos çalışmalarında kullanılan belirsizlik kavramı tesadüfîlik gibi algılansa da kastedilen belirsizlik; gözlemcinin sonucu bilemeyeceğini ifade etmek için kullanılmaktadır yani gözlemci tarafından sonucun bilinmiyor olması esasen sonucun mutlak bilinmez olduğunu göstermemektedir. Bu düşünceyi açıklamaya çalışan Schrödinger’in kendi adını vererek ortaya attığı ve dalga işlevini formülleştirdiği denklemi ile matematiksel formunu alarak kuantum fiziğine girmiş ve daha açıklayıcı hali daha sonraları Schrödinger’in Kedisi adını alan çalışma ile sunulmuştur. Kaos teorisi bu anlamda “yeni bilimin belirsizlik durumuna işaret ederek, diyalektiği yıktığını göstermektedir” (Mermer, 2017).

Schrödinger’in Kedisi, 1935 yılında fizikçi Erwin Schrödinger tarafından tasarlanan ve bazen bir paradoks olarak tanımlanan düşünsel deneydir. Bu deney, günlük nesnelere uygulanan kuantum mekaniğine Kopenhag yorumlamaları ile ilgili sorun olarak gördüğü şeyi ifade etmektedir. Bu düşünsel deneyde, teorik olarak aynı anda hem canlı hem de ölü olabilen hipotetik bir kedi bulunmaktadır ki bu duruma oluşabilecek veya oluşamayacak atom altı bir duruma bağlı olarak oluşan bir durumun sonucu olarak gerçekleşen kuantum süper pozisyonu adı verilmektedir.

Dinamik Sistemler

Matematiksel olarak dinamik sistem, bir fonksiyonun geometrik uzayda bir noktanın zamana bağlılığını tanımladığı sistemdir. Örnek olarak saat sarkacının yaptığı salınım hareketi, bir borudaki sıvının akışı ya da herhangi bir anda bir coğrafyadaki canlı popülasyonları verilebilir. Dinamik sistem, herhangi bir anda, uygun bir durum uzayındaki bir noktayla temsil edilebilen gerçek bir sayılar dizisi tarafından verilen bir duruma sahiptir. Dinamik sistemin evrim kuralı mevcut durumun hangi gelecek durumlar tarafından izlenebileceğini gösteren bir fonksiyondur ve çoğu zaman işlev deterministik olmakla birlikte bazı sistemler stokastiktir. Dinamik sistemlerin incelenmesi matematik, fizik, biyoloji, mühendislik ve ekonomi gibi alanlarda geniş uygulama sahsına sahiptir. Aynı zamanda Kaos Teorisi, lojistik harita dinamikleri, çatallaşma, kendi kendine örgütlenme ve kaos eşiği kavramlarının bir parçasıdır.

Dinamik bir sistemi tanımlayan fark denklemlerindeki doğrusal olmayan bir değişkenden dolayı, önceden bilinemeyen dinamikler meydana gelebilir ki Kaos Teorisi bu tür dinamik sistemleri incelemek için kullanılmaktadır. Karmaşık sistemler, çok sayıda elemanın birbiriyle etkileştiği, pek çok serbestlik derecesi olan yani çeşitli davranış şekilleri gösterebilen, genellikle de dışarıyla madde ve enerji alışverişi yapan, incelenmesi zor sistemlerdir (Yılmaz ve Güler, 2006).

Basit hareketleri temsil eden diferensiyel denklemler ya da denklem sistemleri genellikle lineerdir. Bu denklemlerin çözümü, çözüm uzayı adı verilen analitik fonksiyonlardan oluşan bir uzaydır. Analitik çözümün bulunması demek, ele alınan fiziksel sistemin tamamen bilinmesi demektir. Öte yandan, fiziksel sistem karmaşıklaştıkça, onu temsil eden diferansiyel denklemlerdeki değişkenlerin sayıları (boyut) artar; yani sistem çok değişkenli olur. Ayrıca denklemdeki terimlerin dereceleri yükselir; yani sistem non lineer hale gelir (Karaçay, 2004).

Türbülans

Akışkan dinamiğinde türbülans kavramı basınç ve akış hızında kaotik değişikliklerle karakterize edilen akışkan hareketidir. Bir akışkan paralel katmanlar halinde akarken meydana gelen laminer akışın tam tersi bir durumdur. Doğada meydana gelen akışkan hareketleri genellikle türbülanslıdır. Türbülans düşük viskoziteli sıvılarda yaygın olarak gerçekleşmektedir. Richard Feynman tarafından klasik fizikteki en önemli çözülmemiş problem olarak nitelendirilen türbülansı bir akışkan hareketindeki kinetik enerjinin viskoz sönümleme oranı olan boyutsuz Reynolds sayısı ile tahmin edilebilir. Günlük hayatta türbülansa örnek olarak bacadan çıkan dumanın hareketi, atmosferdeki hava dolaşımları, uçaklardaki açık hava türbülansı ve kan dolaşımı buna örnek olarak verilebilir. Türbülansın Kaos Teorisi ile ilişkisi daha önce belirtilen Üç Cisim Problemi’ndeki cisimlerin yaptıkları hareket ve Ergodik Kuramı ile ilişkilidir.

Tekrarlar (Iteration)

Tekrar, bir sonraki basamak için daha sonraki çıktının girdi olarak kullanılmasında bazı fonksiyonların basitçe tekrarıdır. Temel olarak tekrarlar dönüt halkaları olarak düşünülebilir.

KAOS TEORİSİ VE YÖNETİM

Kaos ve belirsizlik, tüm bilim dallarında bilimsel paradigmayı dönüştürdüğü için kullanılan kavramlardır. Özellikle sosyal bilimlerde yapılan çalışmalarda genellikle laboratuvar ortamında etkenlerin izole edilmesi mümkün değildir ve herhangi bir olay hakkında öngörüde bulunmak için gereken değişken sayısının çok fazla olması ve tüm değişkenlerini içeren bir sistemin oluşturulması imkânsızdır. Sosyal bi­limlerde de, toplumsal olguların tüm değişkenlerini içeren bir sistemin oluşturulması imkânsızdır. Bu durum sosyal bilimlerin doğrusallık ilkelerinden biraz daha uzaklaşmasını ve olay­ları daha karmaşık olgular olarak ele almasını sağlar. Yeşilorman’a (2006) göre kaos, karmaşık ilişkiler düzenini açıklamada sistemleri sadece kendi yapısı içindeki dinamikleri yerine daha büyük bir düzenin bir parçası olarak ele alması ve düzenlilik dışındaki ihtimalleri içermesi bakımından sosyal bilimlere daha önce olmayan önemli imkanlar sağlamaktadır.

Yönetimde kaos teorisinin kullanılmaya başlaması ile birlikte bunu doğuran şartlar ve sürecin ne şekilde gerçekleştiğini anlayabilmek için kaos öncesi ve sonrası yönetim anlayışlarını gözden geçirmek gerekmektedir. Teoriler görüngülere getirilen açıklamalardır ve açıklamayı getiren kişi ve açıklamanın yapıldığı toplumun normları ve değer yargılarından bağımsız değildir. XX. yy’ın başlarında ortaya çıkan kuantum, izafiyet gibi bilimsel kuramların da yine yönetim alanını aynı şekilde etkilemesi kaçınılmaz olmuştur. Bilimde yeni bir oluşum olan kaos teorisi artık otorite ve hiyerarşik ilişkilerden çok, toplumsal aktörler arası bağlantı, etkileşim ve uyumun ön plana çıktığı ve bunun için bireylere daha fazla özgürlük, inisiyatif ve kendini gerçekleştirme imkânının sunulmasını ve yönetimde söz sahibi olmaları gerektiği bakış açısını getirmiştir . Kaos yaklaşımı, egemen yönetim yaklaşımının karşısında, daha esnek, hiyerarşik olmayan soyut bir düşünce niteliğindedir. Bu yeni oluşum, beraberinde yöneticilerin detaylı planlar, denetim ve rutin faaliyetler yerine ekip çalışmasına uygun bütüncül bir yaklaşımla çevresel değişimlere daha kolay uyum sağlayabilecek örgütlenme yoluna gitmeleri gereğini doğurmuştur (Öge, 2005).

Kaotik yönetim yaklaşıma göre bir toplumum yönetsel yapısı, merkeziyetçilikten uzak ve hiyerarşik olmayan, kendi kendini düzenleyen sistemler biçiminde olmalıdır. Kaotik bir yönetsel yapı kurmak bilgi ve habere ulaşıma engellerin kaldırılması ve ortaklaşa kullanılan ve oluşturulan bilgiye güvenilmesi, inovasyon sağlanması, takım çalışmasının teşvik edilmesi ve çeşitliliğin bir zenginlik olarak görülmesi gerekmektedir (Tüz, 2001: 82).

KAOS TEORİSİ VE ÖRGÜTLER

Bir düşünce sistemi olarak kaos ve karmaşıklık kavramları, örgüt sistemlerinde, her sistemin sistem içi ve dışı parametrelerle ilişki içinde olduğunu, bu sebeple “en iyi” dikey ve yatay bir ilişki biçimi belirlenemeyip ilişkilerin yatay, dikey, çapraz ve her yöne olabileceğini savunur. Bu açıdan durumsallık yaklaşımını da benimsediği iddia edilebilir. Örgütlerde hiyerarşik yapıdan şebeke takım çalışmasına geçişin temelinde bu düşünce yapısı olabilir (Koçel, 2015:92).

Örgütlerin değişime ve bilgiye açık olmaları önem taşımaktadır. Değişim, bir tehdit olarak görülmemelidir. Değişime açık örgütler, sadece kendileri için gerekli olan bilgiyi elde etmeye çalışmamalı; aynı zamanda kendilerini dengeden uzaklaştıran, yeniliği arttıran ve bu şekilde gelişmelerini sağlayan her türlü bilgiye her yönden açık olmalılardır. Bu anlamda işletmelerin kaosun kıyısında yaşamalarını sağlayarak onları dengeden uzaklaştıran ve değişim getiren faaliyetlerin, yeniliğin rekabette sürdürülebilir bir üstünlük sağlamak için kullanılan bir araç olduğu bilgi çağında faydalı ve gerekli olduğunu söylemek mümkündür. Değişime açık olmak, kendi kendine örgütlenerek bir düzene ulaşan varlık ve yapıların gelişimi için de önem arz etmektedir. Zira değişime kapalı olmak, kendi kendine örgütlenen bir sistemi bozması açısından tehdit barındırmaktadır (Sayğan, 2014).

Kaos kuramının ortaya attığı görüşler ışığında, değişim için yol gösterici olduğu düşünülen noktalar şunlardır (Çobanoğlu, 2008):

a. Örgütü yeniden düşünmek: Kaosun eşiğine sürüklenen her türlü karmaşık sistemlerde, yeni

b. Yönetme ve “bağlam”ı değiştirme sanatı:

c. Büyük etkiler yaratmak için küçük değişikliklerden yararlanmak

d. Belirmekte olanla doğal bir durum olarak birlikte yaşamak

Literatür örgütsel ortaya mümkün kılan faktörler hakkında bilgi içeriyor olmasına rağmen, bu faktörlere yapılan atıflar çok dağınıktır. Bu yazıda listelenen faktörler doğrudan akademik çalışmalardan ya da kaos ve karmaşıklık teorisi gözetimi altında analiz edilen örgütlere ilişkin çeşitli vaka araştırmalarından dolaylı olarak toplanmıştır. Aşağıda, etkinleştirici faktörlerin bazıları üzerine bir tartışma yer almaktadır:

Az kontrollerle güçlendirme ve yaratıcılık faktörleri: Pascal (1990) ve Stacey (1996), yaratıcılığın aşırı kontrol ve kaos arasında diyalektik bir halde olduğunu öne sürmüştür (Houry, 2012). Acer Group, General Electric ve Sun Microsystems için bir vaka çalışmasına dayanan bir örnek göstermek için, Coleman (1999), üst düzey yöneticilerin refah ve rekabetçiliğin dengesizliği tanımaya ve bunlara toleransa bağlı olduğunun farkına vardıklarını açıklamışlardır. Bu sonuçta bürokratik yapıların genellikle yaratıcılıkları ezdiğini kabul etmelerine yol açmıştır. Bu nedenle, kontrol ve yetkilendirmeyi dengelemek için gevşek bir sistem çerçevesinde güven ve kendine güdüleme dayalı bir felsefe benimsendi. Felsefe deneyim ve yeniliği, başarısızlıkları tolere eden bir sistem olan ödül ve kontrol teşvik sistemi yoluyla teşvik etti. Bu nedenle, bu örnekteki örgütsel ortaya çıkma, çalışanların deneyimlemesine ve yaratmasına izin vermeye dayanıyordu.

Örgütsel biçim faktörü: Miles ve diğ.(1997) bir organizasyonun çevresel uyumunun örgütsel biçimin çalışma mantığına bağlı olduğunu önermişlerdir. Coleman (1999), bu argümanlara paralel olarak, bir organizasyonun, özerk küçük ekiplerle hücresel bir yapı mantığını benimseyip birbirleriyle bilgi paylaşması durumunda, organizasyonun bir bütün olarak daha güçlü olabileceğini belirtti. Bunun nedeni, örgütün esnek hücresel yapısını yenisine dönüştürme yeteneğidir. Bu nedenle, sürekli düzenlemelere daha açık olan yeni bir uyarlanabilir örgütsel formun ortaya çıkması için katı hiyerarşilerden uzaklaşması gerekmektedir.

Otopoetik (kendi kendini yaşatan) geribildirim döngüleri faktörü: Coleman (1999), kendi kendini örgütlemenin yaratıcı girişimciliğin desteğiyle örgütsel bileşenlerin yenilenmesine izin verirken, bir örgüt ve çevresi arasında bir daimi enerji alışverişi gerektirdiğini, çevresel rahatsızlıklar sırasında organizasyonun kimliğini koruduğunu belirtmiştir. Bu enerji değişimi, otopoetik bir geribildirim döngüsü olarak bilinir. Coleman (1999), kendi kendini oluşturan (autopoiesis) tarafından beslenen yaratıcı girişimciliğin kendi kendini örgütleme için bir ön şart olduğunu vurguladı.

Öğrenme topluluğu faktörü: Bir otopoetik geribildirim döngüsü, bilginin geribildirimini işleyebilen bir öğrenme topluluğunun varlığı olmadan etkileyici olmaz. Stewart’a (1997) göre bilgi çalışanları topluluklara katılır, çünkü öğrenecekleri veya paylaşacakları bir şeyler vardır. Coleman (1998) bunu daha da ileri götürerek, bilgi çalışanları arasında kendi kendine örgütlenen davranışın, yeni bilginin öğrenilmesini ve paylaşılmasını sürdüren ve teşvik eden, dolayısıyla ortaya çıkmaya katkıda bulunan teşvikleri dayandırdığını varsaymak için kullanmıştır.

İşlevsel olmayan sistemlerin nihai olarak dağılmasının faktörü (Kaos eşiği faktörü): Sistemler belirli bir zaman periyodu boyunca işlevsel olabilmelerine karşın, ömürleri boyunca yeni çevre şartlarının arkasında durduğu için işlevsizlik dönemine girerler. Bu noktaya gelince, Piotrowski (2006), işlevsiz sistemlerin dağılmasının ve yerinden olmasının stresli koşullara bağlı olarak olduğunu ileri sürdü. Katrina Kasırgası’ndan sonra New Orleans’daki örgütsel işlev bozukluğunun afet ile ilgili literatürde daha önceki araştırmalara dayanarak büyük oranda öngörülmekte olduğunu savundu. Piotrowski (2006)’ye göre insanlar, sosyal ağlar, örgütler, altyapı ve siyasal sistemler sonuçta doğal ve insan kaynaklı felaketlerin sonucunda uyum sağlıyor, yeniden yapılandırılıyor ve işlevsel hale geliyor. Fonksiyonellik için bireysel ve toplu şekilde hareket etme, kısa vadeli karmaşayı ortadan kaldırarak uzun vadeli istikrar ve büyümeyi sağlar. Bu şekilde, sonunda toplumsal kurumlar arasında bir denge durumu korunur. Bu amaçla ve Katrina Kasırgasıyla ilgili olarak yazar, kriz yönetimindeki önemli rolü vurguladı ve yönetim eğitimi ve işletme okulu müfredatında temel olarak olması gerektiğini ifade etmiştir.

İnsanın ihtiyaç duyduğu memnuniyete ilişkin faktör: Coleman (1999), kaos ve düzen arasındaki tekrarlamanın bazılarının arkasında insan ihtiyaçlarının karşılanmasının olduğunu belirtmektedir. Teknoloji şirketlerini kastederek, teknolojinin sadece bir katalizör olduğunu, hızlı değişimin teknoloji kaynaklı olmadığını savunmuştur. Değişim hızı, teknolojinin arkasındaki insanlardan kaynaklanmaktadır, çünkü yeni sebeplerle yeni teknolojiyi kullanma motivasyonu olan kişiler karmaşıklığa neden olmaktadır. Sonuç olarak, en azından teknoloji şirketleri arasında ortaya çıkan kendi kendini organize eden girişimci davranışların kısmen, hedef pazarlarındaki insan ihtiyaçlarını karşılama yönündeki çabalarından kaynaklandığını belirtti. Kahire veya Roma sokaklarındaki trafik sıkışıklığının kaosuna ilişkin Tsoukas’ın (1998), düzen örneğini tekrar gözden geçirmek, trafik kaosundan gelen bir düzenin ortaya çıkmasının, en azından kısmen, insanın ihtiyacını karşılamaya, kaotik trafik koşullarına rağmen sonuçta bir hedefe ulaşma gereksinimine atfedilebileceği düşünülür.

Meşruiyet faktörü: Tornikoski ve Newbert (2007), yeni girişimcilerin stratejik meşruiyet elde etmek için yaptıklarının; geçmişlerini veya sundukları pazarlardan daha önemli olduğunu ileri sürmektedir. Tornikoski ve Newbert (2007), meşruiyet arayışını başarıyla örgütsel ortaya çıkarma ile eşitlemişlerdir. Aynı durum, paydaşların kendilerini meşru olarak algıladıkça gerçekleştirilemeyecek veya ortaya çıkmasına izin verilmeyecek olan yenilikçi fikirler gibi diğer organizasyonel özellikler için de geçerlidir.

Thietart ve Forgues (1995) kaos ve karmaşıklık teorisinin özelliklerini almış ve bunları bir dizi önerme şeklinde örgütsel çalışmalar alanına uyarlamıştır. Bu önermeler aşağıda tablolaştırılmıştır. Örgütlere uygulanan karmaşıklık ve karmaşıklık teorisinin özelliklerini özetlerler.

Tablo 1. Thietart ve Forgues (1995) önermeleri

Önerme 1: Örgütler potansiyel olarak kaotiktir.	Önerme 1a: Bir organizasyonda müdahale eden güçlerin sayısı ne kadar fazla olursa, karmaşa ile karşılaşma olasılığı da o kadar yüksek olur.
	Önerme 1b: Farklı periyodik kalıpları olan kuvvetlerin sayısı ne kadar yüksekse, kaos ile karşılaşma olasılığı da o kadar yüksek olur.
Önerme 2: Örgütler, ayrı bir bifurkasyon(çatallanma) süreci boyunca bir dinamik durumdan diğerine geçmektedir.	Önerme 2a: Bir kuruluş her zaman aşağıdaki hallerden birinde olacaktır: istikrarlı denge, periyodik denge veya kaos.
	Önerme 2b: İki veya daha fazla örgütsel değişken arasındaki gelişen ve sürekli değişen bir organizasyonun, ara periyodik bir davranış yoluyla farklı bir şekilde istikrarlı bir yapıdan kaotik bir duruma geçer.
Önerme 3: Tahmin, özellikle küresel ölçekte ve uzun vadede mümkün değildir.	Önerme 3a: Kaotik bir durumda, diğer tüm unsurlar sabit olduğunda(ceteris paribus), bir değişikliğin etkisi öngörülemeyen uzun vadeli bir etkiye sahiptir.
	Öneri 3b: Bir kaotik durumda, diğer tüm unsurlar sabit olduğunda(ceteris paribus), artan bir değişimin etkisi kısa vadede öngörülebilir.
Önerme 4: Kaotik bir durumda iken, organizasyonlar tanımlanabilir bir düzene doğru çekilmektedir.	Önerme 4a: Kaotik bir durumda, örgütlerin deterministik olarak rastgele bir düzenden çok belirli bir düzeni benimseme olasılığı daha yüksektir.
	Önerme 4b: Bir kuruluşun çevreye açıklığı ne kadar yüksek olursa, organizasyonun belli bir düzene çekilme olasılığı da o kadar yüksektir.
Önerme 5: Kaotik bir durumda iken, örgütler genellikle bir fraktal biçime sahiptir.	Önerme 5a: Kaotik bir durumda, örgütsel, birim, grup ve bireysel seviyelerde benzer yapı kalıpları bulunur.
	Önerme 5b: Kaotik bir durumda, örgütsel, birim, grup ve bireysel düzeylerde benzer süreç kalıpları bulunur.
Önerme 6: Örgütlerin kaotik bir durumda oldukları benzer eylemler hiçbir zaman aynı sonuca yol açmayacaktır.	Önerme 6a: Bir kaotik durumda, aynı organizasyon tarafından alınan iki benzer eylem her zaman iki farklı sonuca yol açar.
	Önerme 6b: Kaotik bir durumda iken, iki örgüt tarafından aynı eylemde bulunmak asla aynı sonuçlara neden olmaz.

Kaos   kuramının  bilim  anlayışında  yarattığı  değişikliğe paralel  olarak,  kaotik  yönetim yaklaşımı  da  yönetim  düşüncesinde  değişiklikler  yaratmıştır. Buna göre analiz yapmak olanaksızlaşmaktadır, neden-sonuç ilişkileri arama çabaları anlamsızlaşmaktadır, geleceğe dair tahminlerde bulunmak imkansızlaştığından ötürü vizyon kavramı kaybolmaya başlamaktadır, fikri çeşitliliğinin olmadığı ve uyum arayan örgütler artık bir fırsat değil tehdit yaratmaktadır ve istatistik biliminin ortaya koyduğu ilişkilere kesinlik içermekten uzaklaşmıştır.

Kaos öncesi ve sonrası örgüt yapılanmalarına bakıldığında mekanik ve organik örgütlerden söz etmek yanlış olmayacaktır. Bu doğrultuda eski paradigmaları kabul eden örgütler mekanik, sistem yaklaşımını içselleştirmiş ve kaotik modellerin evrenin ve sosyal hayatın işleyişinde etkili olduğunu düşünen yeni örgütler organik olarak nitelendirilmektedir. Mekanik örgütler, çok eski bir yapılanma biçimi olan piramit yapıları yani hiyerarşinin ve ast üst ilişkisinin ön planda olduğu yapıları korurken organik örgütler kendi kendine yapılanabilir bir yapıyı benimsemişlerdir. Bu sistemde tüm parçalar değerli ve önemlidir ve bir hiyerarşi söz konusu değildir. Mekanik örgütlerde hüküm süren rol katılığı organik örgütlerde yerini rol esnekliğine bırakmıştır. Organik örgütler lidersizdir ve roller arasında geçiş engelleri bulunmamaktadır. Mekanik yapılar paradoksu inkar ederken organik örgütler paradoks ile yaşarlar ve kaotik bir yapı söz konusudur. Örgüt içindeki tüm farklılıklar zenginlik ve öğrenme fırsatı olarak değerlendirilir. Mekanik örgütler tüm çevre unsurlarına rakip gibi davranırken, organik örgütler zaman içinde rakipleri ile bile stratejik işbirliğine gitmekte sakınca görmezler. Mekanik örgütler çalışanları sınırlandırırken, organik örgütler çalışanlara kendilerini tanıma ve geliştirme fırsatı tanırlar.

SONUÇ

Sosyal bilimlere yönelik post modern paradigmanın temelini oluşturan Kaos Teorisi, örgütlerin ve örgütlerdeki ilişkilerin doğrusal olmayan ve önceden kestirilemeyen bir işleyiş mekanizmasını olduğunu belirtmektedir. Bu sistemlerde kaotik halde bir çok değişken ve etki birbirleriyle sonsuz bağlantı kuran bir kestirilemezlik okyanusu içinde yüzmektedir. Ancak tüm bu belirsizlik hali şaşırtıcı bir şekilde tutarlı ve kararlı bir hal olan düzen olasılığını da içermekte ve bu olasılık yine teorinin sunduğu işleyiş mekanizmasına uygun şekilde belirlenemeyen bir zamanda ortaya çıkarmaktadır.

Kaos Teorisi, örgüte ve karar vericilere bir yeniden düşünme çağrısında bulunmaktadır. Planlama ve analizin gücü bu yeni durumda oldukça sınırlıdır. Liderlik tarihsel vasfını yitirmiş ve örgütlerin her bir parçası eşit öneme sahip hale gelmiştir. Bu yeni paradigma eski mekanik örgüt anlayışına sahip yöneticiler açısından oldukça sahip oldukları anlayışa karşı sert ve kırıcı sonuçlar doğurabilir. Strateji belirleme konusundaki başarısızlıklar yine durağan sistemlere alışkın yöneticiler açısından kaçınılmaz bir sonuç olacaktır. Uzun vadeli stratejiler yerini mutlaka çevre ile değişebilen ve dönüşebilen strateji, amaç, hedef ve taktiklere bırakmalıdır.

Çevresine uyum sağlayamayan herhangi organik yapının yaşama şansı bulunmadığı gibi, bu örgütsel ekoloji için de geçerli bir durumdur. Belirsizlik, sürekli değişim ve devinim kaotik yapılarla birleştiğinde eski kabullerle tehdit olarak görülen birçok durum değerlendirilebilecek fırsatlar haline gelmekte ve bunun tam tersi de yine geçerli olmaktadır. Kaos düşüncesi ve evrenin insanoğlunun sadeleştirdiği ve basitleştirdiği halinden uzak çalışma prensipleri belki de yöneticileri tarih boyunca karşı karşıya kalmadıkları bir meydan okuma ile yüzleşmek zorunda bırakmaktadır.

REFERANSLAR

Altunoğlu, S. (2009)  Go Sorunsalı ve Kaotik Çözüm Arayışları, Bibliothec Felsefe ve Sosyal Bilimler Dergisi, Bahar .

Çavuş F., İnce Z., Yakut E., Akbulut, M., Güloğlu, E., Kalkan, A. (2016). Kaos ve Durumsallık: Bir Değerlendirme, Kahramanmaraş Sütçü İmam Üniversitesi Sosyal Bilimler Dergisi, 13:2.

Erdoğan, H. (2012) Karmaşa, Karmaşıklık ve Eğitim İlişkisi, Tarih, Kültür ve Sanat Araştırmaları Dergisi.

Kendirli, S. (2006). Portföy Yönetiminde Kaos Teoremi.Journal of İstanbul Kültür University, 2006:2.

Mutlu, A. (2006). Ekolojik Düşüncede Kaotik Eğilimler.Journal of İstanbul Kültür University, 2006:2.

Öge,S. (2005). Düzen Mi Düzensizlik (Kaos) Mi? Örgütsel Varlığın Sürdürülebilirliği Açısından Bir Değerlendirme. Selçuk Üniversitesi Sosyal Bilimler Enstitüsü Dergisi, (13), 285-303.

Uçar, S. (2010). Kaos Teorisinin Felsefi Özellikleri, Yayınlanmamış Yüksek Lisans Tezi, İstanbul Üni. Sosyal Bilimler Enstitüsü.

Cramer, F. (1998) Kaos ve Düzen Sırat Köprüsündeki Hayat. (Çev.Veysel Atayman). İstanbul: Alan Yayıncılık.

Ruelle, D. (1999). Rastlantı ve Kaos. İstanbul: Tubitak Popüler Bilim Kitapları:7. 12. Basım.

Koçak, K. (2000) Kaos ve Atmosfer. Tübitak Bilim ve Teknik. (391).

Hun, K. (2009) “Kaos ve Kaos Teorisi”, (Çevrimiçi), http://www.aninda tepki.com/genel-bilim/kaos-ve-kaos-teorisi/ adresinden erişilmiştir.

Akmansoy, V., Kartal, S. (2014). Kaos Teorisi ve Eğitime Yansımaları: Mehmet Akif Ersoy Üniversitesi Örneği, Kuram ve Uygulamada Eğitim Bilimleri Dergisi.

Dereli, T., Durmuşoğlu, A. ve Kanat, Ş. (2006) “İşletmelerde Kaos Yönetimi”, Journal of İstanbul Kültür University, 3:2.

Çobanoğlu, F. (2008) Değişim Mantığını Anlamak: Akış ve Dönüşüm Olarak Örgüt, Pamukkale Üniversitesi Eğitim Fakültesi Dergisi Yıl 2008 (1) 23. Sayı

Altun, S. (2001). Kaos ve Yönetim Kuram ve Uygulamada Eğitim Yönetimi. Sayı:2b.

Rockler, M. J. (1990~199l). Thinking About Chaos: Non-Quantitative Approach To Teacher Education. Action in Teacher Education, XII(4), 56-63.

Tüz, M. V. (2001) Kaos Ortamında Self Organizasyon Davranışı, Alfa Basım Yayım Dağıtım Ltd. Şti., İstanbul.

Mermer, A. (2017) Yeni Bilim Paradigmasi ve Kaos Teorisi Perspektifinden Halkla İlişkiler, Akademik Sosyal Araştırmalar Dergisi, Yıl: 5, Sayı: 63, Aralık 2017.

Gleick, J. ve Berry, M. (1987). “Chaos-Making a New Science” Nature,(5), 293-330.

Gleick, J. (1995) (çev. Fikret Üçcan), Kaos, Tübitak Popüler Bilim Kitapları, Ankara.

Griffiths, D.E., Hart, A.W., & Blair, B.G. (1991). Still Another Approach to Administration: Chaos Theory. Educational Administration Quarterly, 27(3).

Fındık, O. (2004). Şifrelemede Kaotik Sistemin Kullanılması, Yayımlanmamış Yüksek Lisans Tezi, Selçuk Üniversitesi, Fen Bilimleri Enstitüsü.

Diker Çamlıbel, N. (2003) Belirsizlik Ortaminda Planlama Düşüncesi ‘Sinerjetik Toplum – Sinerjik Yönetim ve Sinerjist Planlama Modeli’ Örnek Olay: 17 Ağustos – 12 Kasim 1999 Depremleri Sonrasi Kaos Ve Kendi – Kendine Organizasyon Süreci, Doktora Tez, Yıldız Teknik Üniversitesi, Fen Bilimleri Enstitüsü.

Kılıç, B. (2010) Kaos Teorisi ve Ekonomiye Uygulanabilirliği Üzerine Bir Yaklaşım, Yüksek Lisans Tezi, İstanbul Üniversitesi, Sosyal Bilimler Enstitüsü.

Boeing, G. (2016). “Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction”. Systems. 4 (4): 37.

Ural, Ş. (2009). Kozmostan Kaosa, https://www.safakural.com/makaleler/kozmozdan-kaosa adresinden erişilmiştir.

Biçici, F. (2016) Kaos Teorisi, Determinizm ve Yeni Bilim Paradigması Sürecinde Sosyal Bilimler ve Turizm Araştırmaları Açısından Önemi, Turizm Akademik Dergisi.

Farazmand, A. (2003). Chaos And Transformation Theories: A Theoretical Analysis With Implications For Organization Theory And Public Management. Public Organization Review: A Global Journal, 3, 339-372.           

Öztaş, N. (2015) Örgüt, Örgüt ve Yönetim Kuramları (II), Otorite Yayınları.

Styhre, A. (2002). Non-linear Change in Organizations: Organization Change Management Informed by Complexity Theory. Leadership and Organizational Development Journal, 23.

Amagoh, F. (2008). Perspectives on Organizational Change: Systems and Complexity Theories. The Innovation Journal: The Public Sector Innovation Journal, 13.

Alpar, O. (2012). Kaos Teorisi ve Kaotik İşletme Uygulamaları, İstanbul Üniversitesi SBE Doktora Tezi.

Tosun, T. (2006). Türev Araçlar, Kaos Teorisi Ve Fraktal Yapıların Vadeli İşlem Zaman Serilerinde Uygulanması, İstanbul.

Karaçay, T. (2004). Determinizm ve Kaos. Mantık, Matematik ve Felsefe II.Ulusal Sempozyumu, Assos.

Yılmaz, D. ve Güler, N. F. (2006). Kaotik Zaman Serisinin Analizi Üzerine Bir Araştirma, Gazi Üniv. Müh. Mim. Fak. Der. Cilt 21, No 4, 759-779, 2006

Yeşilorman, M. (2006). Kelebek Kanadını Kimden Yana Çırpıyor? Birleştirilmiş Bilimin Kıyısında Kaos ve Sosyal Bilimler. Journal of İstanbul Kültür University, 3:77-86.

Wichmann, E. (1993). Kuantum fiziği: Berkeley fizik dersleri. (Çev. T. N. Durlu ve Y. Elerman). Ankara: Bilim Yayınları.

Koçel, T. (2015) İşletme Yöneticiliği, Beta Yayınları.

Sayğan, S. (2014) Örgüt Biliminde Karmaşıklık Teorisi, Ege Akademik Bakış, Cilt: 14:3.

Houry, S. A. (2012) Chaos and Organizational Emergence: Towards Short Term Predictive Modeling to Navigate a Way Out of Chaos, Systems Engineering Procedia 3 (2012)

Pascale, R.T. (1990). Managing at the edge of chaos. New York: Simon and Shuster.

Stacey, R.D. (1996). Complexity and Creativity in Organizations. San Francisco, CA: Berrett-Koehler

Piotrowski, C. (2006). Hurricane Katrina and organization development: Part 1 Implications of chaos theory. Organization Development Journal, 24(3), 10-19.

Coleman, H.J. Jr. (1999). What enables self organizing behavior in businesses? Emergence,1 (1), 33-48.

Miles, R.E., Snow, C.C., Mathews, J.A., Miles, G. & Coleman, H.J. Jr. (1997). Organizing in the knowledge age: Anticipating the cellular form. Academy of Management Executive, 11(11), 7-24.

Stewart, T.A. (1997). Intellectual capital: The new wealth of organizations. New York: Currency Doubleday.

Tornikoski, E.T. & Newbert S.L. (2007). Exploring the determinants of organizational emergence: A legitimacy perspective. Journal of Business Venturing, 22, 311-335.

Thietart, R. & Forgues, B. (1995). Chaos Theory and Organization. Organization Science, 6(1), 19-31.

Kaçmaz, G. (2005). Kaos Teorisi ve Sosyolojisi: Toplumların Denetlenmesinde Yeni Bir Adım İstanbul Üniversitesi Sosyal Bilimler Enstitüsü Sosyoloji Anabilim Dalı Yüksek Lisans Tezi, İstanbul