Örnekleme

Veri (İng. ve Lat. datum; çoğul data) bir ham (işlenmemiş) gerçek ya da enformasyon parçacığına verilen addır.

Veriler ölçüm, sayım, deney, gözlem ya da araştırma yolu ile elde edilmektedir. Ölçüm ya da sayım yolu ile toplanan ve sayısal bir değer bildiren veriler nicel veriler, sayısal bir değer bildirmeyen veriler de nitel veriler olarak adlandırılmaktadır. Her sembolik gösterim gibi, veri de belirli bir nesne, birey ya da olguya ilişkin bir soyutlamadır. Ancak enformasyon ve bilginin soyutluk düzeyleri ile karşılaştırıldığında, verilerin soyutluk düzeyi daha düşüktür. Bir verinin tek başına bir anlamı ve işlevi bulunmamaktadır. Veriler toplandıktan sonra gruplanarak, sıralanarak ve özetlenerek, elle ya da bilgisayarla işlenip enformasyona dönüştürüldüklerinde anlam kazanmakta; ait oldukları bağlamı açıklama gücüne kavuşmaktadır. Problem çözme ya da karar verme gibi bir amaca hizmet edebilecek duruma gelmektedir.

Her araştırmada temsil yeteneğine sahip bir örneklem seçmek temel ilkedir. Temsil yeteneğine sahip bir örneklemin temel özellikleri şunlardır. Örneklemin büyüklüğü yeterli olmalıdır. Örneklem evrendeki dağılıma çeşit ve oran yönünden benzer olmalıdır. Örneklem olasılıklı örnekleme yöntemlerinden biriyle seçilmelidir. Örneklem seçiminde taraf tutulmamalıdır.

Örneklem alınan ve alınmayan birimlerin ortaya çıkardıkları şansa bağlı toplam hata miktarıdır. Bu miktarı gösteren ölçüt ‘standart hata’dır.

EVREN : Araştırmadan elde edilen sonuçların genellemesinin istendiği bütün.

ÖRNEKLEME: Örneklemin belirlenmesi için kullanılan yöntemler topluluğu. Bütün evreni yansıtabilecek, evrenin bir kısmını seçme işlemidir. Örnekleme ile yapılacak bir araştırmanın en önemli özelliği evrendeki gerçek durumu ortaya çıkarabilmesi için  en önemli koşul örneklemin evreni temsil edebilmesidir.

ÖRNEKLEM: Araştırma evreninden belirli kıstaslara göre seçilen kesiti oluşturan ve aynı özelliklere sahip kişilerin bir araya getirdiği grup.

Örneklemin Belirlenmesi

Dikey yöntem ile örneklem belirleme ,genelden başlayarak özele doğru inilmesidir. Örneğin yaşam kalitesi üzerine araştırma yapmayı düşünen bir araştırmacı, evren olarak ülkede yaşayan tüm insanları alan grup, daha sonra evrenin içinden öğretmenleri daha sonra orta öğretim öğretmenlerini en son olarak da pozitif bilimler dersi öğretmenlerini seçebilir.

Yatay yöntem ile örnekleme yönteminde ise üniversite öğrencileri evren kabul edildiğinden sadece belirli bir üniversitenin öğrencileri ya da farklı üniversitelerin aynı fakültesinde öğrenim gören öğrencileri örneklem alınabilir.

Yöntem	Örneklem
Görüşme Yöntemi	12-15(YL) 20-30(Doktora ve diğer)
Gözlem Yöntemi – Katılımcı Gözlem  Yöntemi	Farklılık gösterebilir, kesin sınırları yoktur.
Arşiv/doküman İnceleme Yöntemi	Çalışılacak konunun içeriğine ve kaynakların ulaşılabilirliğine göre değişkenlik gösterir.
Örnek Olay Yöntemi	1 – Yeterli >1 – Olanak ve zamana bağlı
Odak grup Yöntemi	< 1 gün – 8-12 > 1 gün – 20-25
Açık Uçlu Soru Formu	Min. 50 Max. 120-150 Daha fazlası verinin sağlıklı analizini zorlaştırır.

Örneklemin çok küçük olması durumunda araştırma sonuçlarının evren için genellenebilmesi güçleşir. Betimsel araştırmalarda minimum %10 örneklem alınır, küçük evrenlerde ise %20’ye ihtiyaç duyulur. Korelasyon çalışmalarında en az 30, nedensel kıyaslamalarda her gruptan en 30’ar eleman gereklidir. Deneysel araştırmalarda ise, her grupta 15’er denek gibi az sayıda denek olması sonuçların geçerli olmasını sağlayabilir. Bazı çevreler ise deneysel araştırmalarda her grupta en az 30’ar deneğin bulunmasını önermektedir. Ancak örnek büyüklüğünün fazla olması fazla olması sonuçların güvenilirliğini arttırır.

Evren Büyüklüğü	Kesinlik ( Göz Yumulabilir Hata )
	+ 1%	+ 2%	+ 3%	+ 4%	+ 5%
1.000	**	**	**	**	400
2.000	**	**	959	683	498
3.000	**	**	1142	771	544
4.000	**	**	1262	824	569
5.000	**	2267	1347	859	586
10.000	**	2932	1556	939	622
20.000	9068	3435	1688	986	642
50.000	12456	3830	1778	1016	655
100.000	14229	3982	1810	1026	659
500.000 to ¥	16056	4113	1836	1035	663

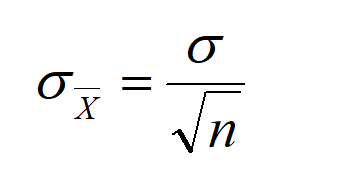
ifadesinden çekilerek ;

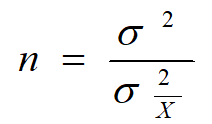
şeklinde hesaplanır. Örneklem hacminin büyümesi, ortalamaların örnekleme dağılımının standart sapmasının azalmasına sebep olur.

Örnek

Bir tır lastiği fabrikası , bir lastiğin ortalama dayanıklılık gücünü tahmin etmek istiyor. Önceki test sonuçlarına göre kabul edilebilir standart sapma değeri 70 psi olarak belirlendiğine ve standart hatanın 20 psi olması istendiğine göre örneklem büyüklüğü ne olmalıdır?

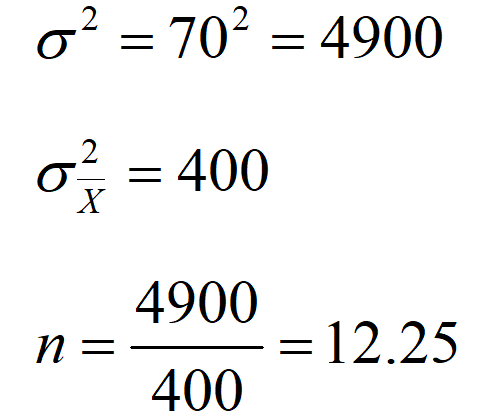
Örnek Hacmi Belirleme (populasyon ortalamasının tahmini için)

Normal dağılış varsayımı altında ortalama için (1 – α) güven sınırları, izin verilecek hata miktarı L olsun. Buradan n çekilirse, örnek büyüklüğü aşağıdaki gibi hesaplanabilir:

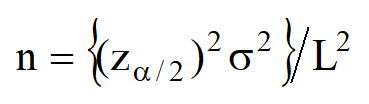
Bir üretim sürecinde üretilen çivilerin boyları, standart sapması 1.8 milimetre olan normal bir dağılıma uymaktadır. Üretim sürecinde ortalamanın iki yanında en çok 0.50 mm uzanan bir %99 güven aralığı istenirse bu aralığa ulaşmak için örnek büyüklüğü kaç olmalıdır?

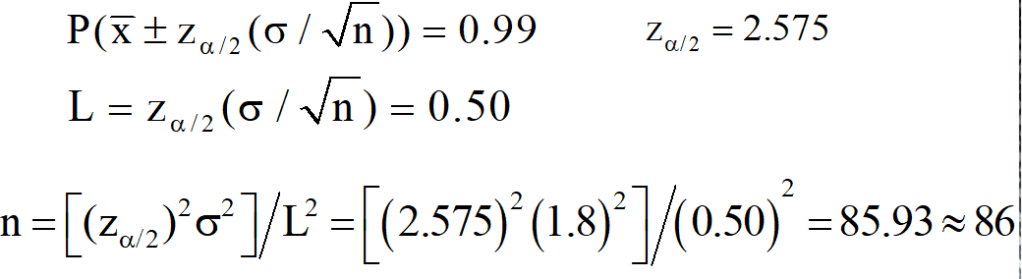
Örnek Hacmi Belirleme (populasyon oranının tahmini için)

Bir siyasetçi, tartışmalı bir yasa tasarısını savunan seçmenlerinin oranını tahmin etmek istemektedir. Örneklem oranının her iki yanında en çok 0.05 uzanan bir %99 güven aralığı isteniyor. Bunun için kaç örneklem gözlemi gerekir?

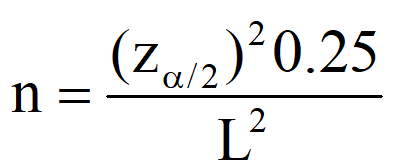
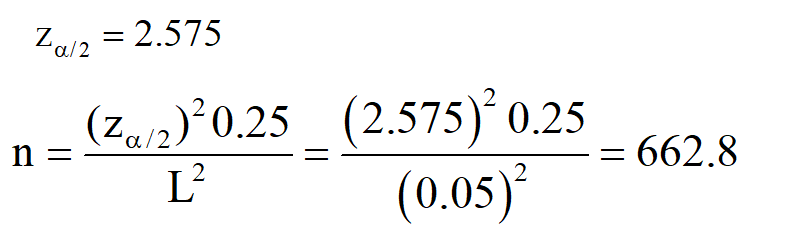
Olasılığa Dayalı Yöntemler

Basit Tesadüfi Örnekleme

Basit rasgele örneklem almanın ana prensibi her bir anakütle elemanının aynı olasılıkla örneğe girebilmesidir. Bu bir olasılık örneği tanımına uyar, çünkü her bir anakütle elemanı için örneklemde bulunma olasılığı bir Bernoulli dağılımı gösterir. Eğer anakütle büyüklüğü N ile ifade edilirse, her bir anakütle elemanı 1/N olasılıkla örnekte bulunur.

Bu prensibi uygulamak için şu aşamalar uygulanır:

§Ana kütlenin her bir elemanı tespit edilir ve tespit edilen elamanların her birine bir sayısal kod verilir. Genellikle kodlar birbirini takip eden sayılar halinde sıralama düzeni halindedir ve sanki sayısal bir isimdir.

§İkinci aşamada en uygun örneklem hacmi, yani n, tayin edilir.

§Bir rastgele numara üretici alet kullanılarak istenilen n sayıda (birbirinden değişik olması tercih edilir) rastgele sayı çıkartılır. Rassal sayılar gayet çok olduğu için bir çeşit geri koymadan örnek alma deneyim sonucu olan n tane rasgele sayı aynı olasılığa haizdir.

§Bu rastgele n numara anakütle elemanlarının kodları ile karşılaştırılır. Kod numarası, çekilmiş olan rasgele sayıya eşit olan elemanlar örnek elemanı olarak seçilirler.

Yöntemin Yararlı Yönleri

§Evrendeki her elemanın eşit seçilme şansı vardır

§ Evren çok büyük ve karmaşık değilse seçme işlemi kolaydır

§Bu yöntemle yapılan örneklemede istatistiksel işlemler ağırlıksız olarak yapıldığı için değerlendirme işleminde kolay olur.

Yöntemin Sakıncalı Yönleri

§Evren çok büyükse evreni listelemek ve seçmek güçtür.

§İncelenen özellik evrendeki elemanların bazı özelliklerine göre değişiklik gösterebilir.

§Örnekleme seçilecek bireyler çok geniş bir bölgede dağınık bir şekilde yerleşmiş  olabilirler.

Tabakalı Rastgele Örnekleme Yöntemi:

İncelenen karakter deneklerin herhangi bir özelliğine göre değişiklik gösteriyorsa        ( yaş, cinsiyet, sosyo-ekonomik, kültürel özellikler vb.) tabakalı rastgele örnekleme yöntemiyle örnekleme yapmak daha doğru sonuç verebilir. Bu yöntemin etkin olabilmesi için tabakalardaki birimlerin kendi içinde homojen olması ve tabakalar arasında gerçek bir farklılık bulunması gerekir.

Örneğin bir ilköğretimdeki çocukların boy uzunlukları ölçülmek  istenirse, yaş ile boy  arasındaki ilişki dikkate alınmalıdır. Örnekleme girecek çocuklar, yaşları dikkate alınmadan basit rastgele yöntem ile seçilirse elde edilecek sonuçlar gerçeği yansıtmayabilir. Çünkü şans eseri küçük yaştakiler yada büyük yaştakiler seçilen örneklemde daha fazla sayıda bulunabilir. Çocuklar, önce yaşa göre tabakalanıp, her tabakadan basit rastgele örnekleme yöntemiyle belirli sayıda seçilirse sonuç gerçeğe daha yakın olur. 

Her tabakaya eşit sayıda birey düşmesi olanaksız olacağından, her tabakadan kaç bireyin örnekleme alınacağı sorunu çıkar. Bu durumda iki yol izlenebilir. Birincisinde, tabakalardaki birey sayısı göz önüne alınmadan her tabakadan eşit sayıda birey örnekleme alınır. Buna orantısız seçim denir. Orantısız seçimde istatistiksel değerlendirmenin kesinlikle ağırlıklı olarak yapılması gerekir. İkincisinde ise, örnekleme alınacak bireyleri tabakalardaki birey sayısına orantılı olarak seçmektir. Başka bir deyişle, çok kişi içeren tabakadan çok, az kişi içeren tabakadan az kişiyi örnekleme almaktır. Örneklem seçimi orantılı yapıldığında aritmetik ortalama ağırlıksız, standart sapma ise ağırlıklı olarak hesaplanır. Orantılı seçim, işlemleri kolaylaştırdığı için tercih edilen bir yoldur.

Küme Örnekleme Yöntemi:

Bu yöntemde örnekleme birimi tek kişi yada aile değil bir grup, demet ya da kümedir. Araştırma yapılacak bireyler  geniş bir alana dağılmış durumda iseler, basit rastgele ve tabakalı rastgele örnekleme yöntemiyle yapılan seçimle örnekleme çıkan bireylere ulaşmak pratik olmayabilir.  Böyle bir durumda küme örnekleme yöntemi uygulama kolaylığı sağlar. Bu yöntemde örneklem hatası büyük olabilir.

Örneklem hatasını etkileyen en önemli faktör kümelerin homojen ya da heterojen olmasıdır. Küme içinin heterojen olması( değişik özellikteki birimleri içermesi) durumunda örneklem hatası küçülür. Küme içindeki birimlerin homojen olması durumunda ise örneklem hatası büyük olur.

Küme örnekleme yönteminde genel kural kümedeki birim sayısının az olması yani kümelerin küçük olmasıdır. Kümelerin küçük olması küme sayısını artıracak, bu da değişik özellikteki kümelerin örnekleme girme şansını arttıracaktır. Örneğin 4 000 aile içeren bir bölgeyi 800’er ailelik 5 kümeye ayırıp buradan 1 kümeyi örnekleme alma yerine, 200’er ailelik 20 kümeye ayırıp 4 küme seçmek daha uygundur.

Sistematik Örnekleme Yöntemi:

§Örneklem seçim işlemlerinin kolay olması nedeniyle özellikle evren büyük olduğunda kullanılan bir örnekleme yöntemidir. Bu yöntemin en çok kullanıldığı durumlar:

§Çok sayıda birim içeren kayıt sistemlerinin incelenmesinde. Örneğin, hasta dosyaları, hasta ya da işçi kayıtları, kayıt defterleri, fişler , listeler gibi.

§Birim sayısı çok fazla olduğu için listelenmesi güç ya da olanaksız olan durumlarda.  Örneğin, büyük bir kentte ev seçimi, sokak seçimi, işyeri seçimi otomobil seçimi gibi.

§Seçim işlemlerinde evren büyüklüğü( N ) örneklem büyüklüğüne ( n ) bölünerek kaç birimde bir birimin örnekleme alınacağı saptanır. Örneğin, 24 000 hasta dosyası bulunan bir arşivden 800 dosya örnekleme seçilecekse ( 24 000 / 800  = 30 ) her 30 dosyada bir dosya örnekleme alınacaktır. Başlangıç sayısı rastgele sayılar tablosundan 1 – 30 arasında bir sayı seçilerek bulunur. Seçilen sayı 7 ise önce 4’üncü dosya örnekleme alınır, sonra her 30 dosya 1 dosya örnekleme alınır. Böylece örnekleme çıkan dosya numaraları 7, 37, 67, 97, ……14 977 olacaktır.

Olasılığa Dayalı Olmayan Yöntemler

Kolayda (Gelişigüzel) Örnekleme Yöntemi: Bu tür örnekleme, araştırmacının saptanan örneklem büyüklüğüne göre herhangi bir şekilde evrenin bir parçasını seçmesidir.

Amaçlı (Kasıtlı) Örnekleme. Bu örneklemenin temeli, araştırmanın amaçları doğrultusunda bir evrenin temsilci bir örneği yerine, kasıtlı olarak bir ya da birkaç alt kesimini örnek olarak almaktır.

.Kota örnekleme. Kota örneklemede sınırlı bir evren, araştırmanın amacına uygun olarak araştırmacının öngördüğü belirli değişkenlere göre sınıflandırılır.

Kartopu örnekleme. Kartopu örneklemede öncelikle evrene ait birimlerden birisi ile temas kurulur. Temas kurulan birimin yardımıyla ikinci birime, ikinci birimin yardımıyla üçüncü birime gidilir.